第 16 章 终身学习

终身学习本质上基于人类对于人工智能的想象，期待人工智能可以像人类一样能够持续不断地学习。

16.1 灾难性遗忘

如图 16.1 所示，我们先训练机器做任务一语音识别，再教它做任务二图像识别，接着再教它做第三个任务翻译，这样一来它就一起学会了这三个任务。我们不断去教会机器学习新的技能，等它学会成百上千个技能之后，它就会变得越来越厉害，以至于人类无法企及，这就是我们所说的终身学习（LifeLong Learning，LLL）。

终身学习也称为持续学习（continous learning）、无止尽学习（never-ending learn-ing）、增量学习（incremental learning）。

图 16.1 自监督学习框架

读者可能会疑惑，这个终身学习的目标过于远大，并且难以实现，其意义又在哪里呢？其实在真实的应用场景中，终身学习也是派得上用场的。举例来说，如图 16.2 所示，假设我们首先通过收集一些数据然后训练得到模型，模型上线之后它会收到来自使用者的反馈并且得到新的训练数据。这个时候我们希望能够形成一个循环，即模型上线之后我们得到新的数据，然后讲新的数据用于更新我们的模型，模型更新之后又可以收到新的反馈和数据，对应地再次更新我们的模型，如此循环往复下去，最终我们的模型会越来越厉害。我们可以把过去的任务看成是旧的数据，把新的数据即来自于反馈的数据，这种情景也可以看作是终身学习的问题。

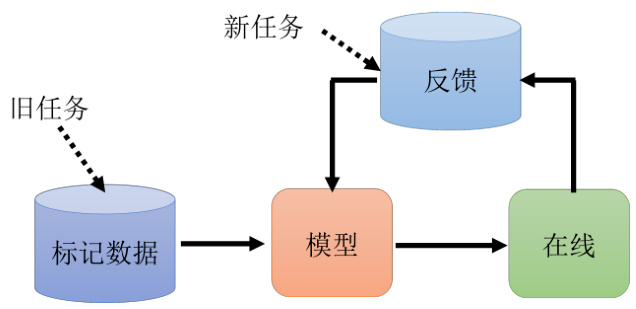
图 16.2 自监督学习框架

终身学习有什么样的难点呢？看上去不断更新它的数据和对应网络的参数就能实现终身学习，但实际上没有那么容易。我们来看一个例子，如图 16.3 所示，假设我们现在有两个任务，第一个任务是手写数字识别，给一张包含噪声的图片，机器要识别出该图片中的数字 ${}^{\leftarrow }{0}^{}$ ，第二个任务也是手写数字识别，只是给的图片噪声比较少，相对来说更容易。当然有读者可能会认为这不算两个任务，最多算同一个任务的不同域，这样说也没错。可能读者想象中的终身学习应该是先学语音识别然后图像识别之类的，但其实现在的终身学习都还没有做到那种程度。目前关于终身学习的论文中所说的不同任务大概指的就是本示例中同一个任务的不同域这种级别，只是我们把它们当作不同的任务来对待。但即使是非常类似的任务，在做终身学习的过程中也会遇到一些问题，具体哪些问题我们接下来一一说明。

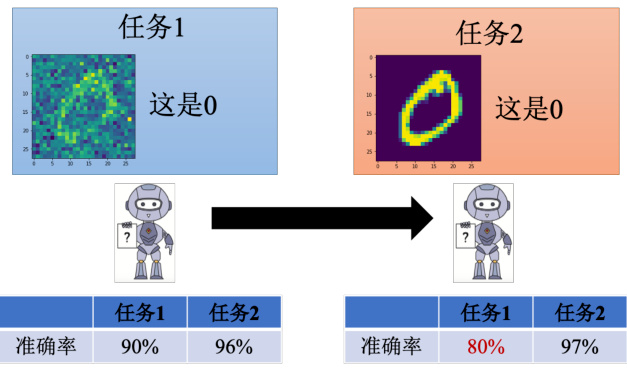
图 16.3 自监督学习框架

我们先训一个比较简单的网络来做第一个手写数字识别任务，然后再做任务二，任务一上的准确率是 $90\mathrm{\%}$ ，此时就算没有训过任务二，在任务二上也已经有了 $96\mathrm{\%}$ 的准确率，可以说迁移得非常好，说明能够解决任务一，相应地也能解决任务二。那么接下来我们用同一个的模型，即在任务一中训练好的模型再去训练任务二，结果我们发现在任务二上的准确率变得更好了（ $97\mathrm{\%}$ ）。但是比较糟糕的事情是此时机器已经忘了怎么去做任务一了，即在任务一上的准确率从 $90\mathrm{\%}$ 降到了 $80\mathrm{\%}$ 。有读者可能会想是不是网络设置的太过简单然后导致出现这样的现象，但实际上我们把任务一和任务二的数据放在一起让这个网络同时去学的时候，会发现机器是能够同时学好这两个任务的，如图 16.4 所示。

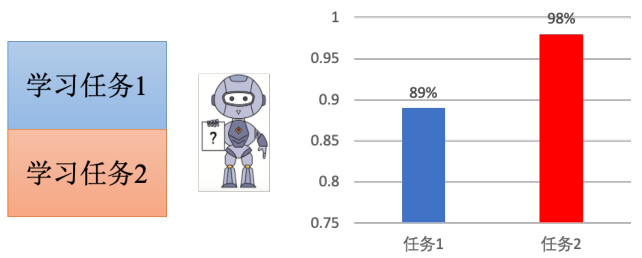
图 16.4 自监督学习框架

接下来举一个自然语言处理方面的例子，即 QA 的任务，QA 指的是给一篇文档，模型训练之后能够基于这个文档回答一些问题。当然为了简化，我们会将一个更简单的实例，即“bAbi”，它是一类非常早期和基础的研究任务，总共有二十个子任务。

如图 16.5 所示，其中第五个任务是给了三个句子，即 Mary 把蛋糕给了 Fred，Fred 把蛋糕给了Bill，Bill 给了牛奶给Jeff，最后问“谁给了蛋糕给 Fred？"类似于这种简单问题，其他任务包括第十五个任务也同理。我们的目标是让 AI 依次去学这二十个任务，要么让一个模型同时学这二十个任务，要么用二十个模型，每个模型分别学一个任务，这里我们主要讲的是前者。最后我们实验的结果如图 16.6 所示。

图 16.5 bAbi 任务示例

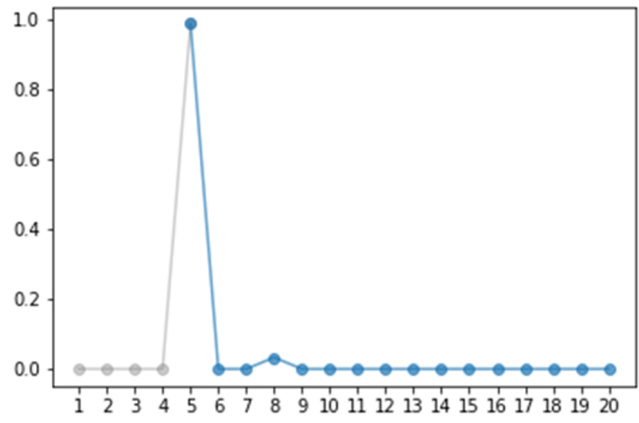
图 16.6 任务 5 的准确率（依次学习 20 个任务）

可以看到，一开始我们没有学过任务五，所以准确率是零。当开始学第五个任务之后，准确率达到百分百，然而开始学下一个任务的时候，准确率就开始暴跌，即学习新的任务之后一下子就完全忘了前面的任务。读者可能以为模型本身就没有学习那么多任务的能力，但其实不是的。如图 16.7 所示，当模型同时学二十个任务的时候，我们会发现机器是有潜力能够学习多个任务的，当然这里第十九个任务可能有点难，模型的准确率非常低。

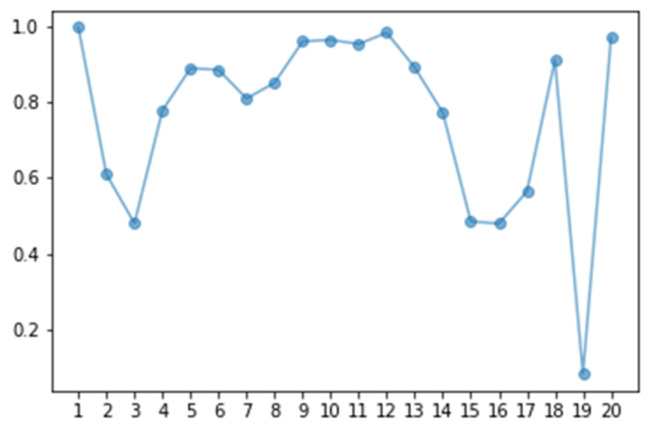
图 16.7 所有任务的准确率（同时学习 20 个任务）

当模型依次学习多个任务的时候，它好像一个上下两端都接有水龙头的池子，新的任务从上面水龙头进来，旧的东西就从下面水龙头那里冲掉了，永远学不会多个技能，这种情况称为灾难性遗忘（catastrophic forgetting）。我们知道即使是人类也可能会有遗忘的时候，而这里在遗忘前面我们加上了灾难性这个形容词，意在强调模型的这个遗忘不是一般的遗忘，而是特别严重程度的遗忘。

讲到这里我们接下来就需要知道怎么去解决这个灾难性遗忘的问题了。在我们讨论具体的技术之前，也许读者会有这样一个问题。刚才我们的例子有提到模型是能够同时学多个人任务的，这种学习方式称为多任务学习（multitask learning），既然有这个多任务学习的例子，那为什么还要去做终身学习的事情呢？但其实这种多任务学习会有这样一个问题，加上我们需要学习的任务不再是简简单单的二十个，而是一千个，那么我们在学第一千个任务的时候，按照这个逻辑还得把前面九百九十九个任务的数据放在一起训练，这样需要的时间是比较久的。

就好比假设一个人要学一门新的课程，那他就必须要把这辈子上过的所有课程都学过一遍才有办法学习新的任务，这样其实是比较低效的。而且随着要学习的任务越来越多，所需要的训练时间也会越来越长。但如果我们能够解决终身学习的技术，那么其实就能够高效地学习多种新任务了。当然这种多任务学习也并非没有意义，我们通常把多任务学习的效果当成终身学习的上界，即我们在做终身学习的时候往往会先跑一个多任务学习的结果，来帮助我们参考终身学习的上限在哪里。

这里可能读者又会有一个问题，即为什么我们不能每个任务都分别用一个模型呢？其实这样做会有一些问题，首先这样做可能会产生很多个模型，这样对机器存储也是一个挑战。另外不同任务之间可能是有共通的，从任务 A 学到的数据也可能在学习任务 B 的时候有所参考。类似的还有一个迁移学习的概念，虽然终身学习和迁移学习都是让模型同时学习多个任务，但它们的关注点是不一样的。在迁移学习中，我们在意的是模型在前一个任务学习到的东西能不能对第二个任务有所帮助，只在乎新的任务做得如何。而终身学习更注重的是在解决完第二个任务之后能不能再回头解决第一个任务。

16.2 终身学习评估方法

现在我们可以先看看怎么评判终身学习技术做不做得好的一些标准。在做终身学习之前，得先有一系列任务让模型去学习，其实通常都是比较简单的任务。如图 16.8 所示，任务一就是常规的手写数字识别，任务二其实还是手写数字识别，但只是把每一个数字用某一种特定的规则打乱，称之为排列，这种算是比较难的，还有更简单的就是把数字右转一次。

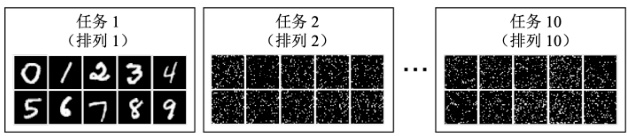
图 16.8 终身学习手写数字识别示例

具体的评估方式如图 16.9 所示，首先有一排任务，并且有一个随机初始化的参数，用在这 $T$ 个任务上，得到对应的准确率。然后让模型先学第一个任务，然后在所有任务上分别测一次准确率，即 $R_{1,1},...,R_{1,T}$ ，依此类推。直到学完所有的任务，得到一个准确率的表格，来评估终身学习的结果。

具体的最终准确率公式表示为

$$\frac{1}{T}\sum _{i=1}^T{R}_{T,i}$$

另一种评估方法叫做反向迁移，即

$$\frac{1}{T-1}\sum _{i=1}^{T-1}{R}_{T,i}-R_{T,i}$$

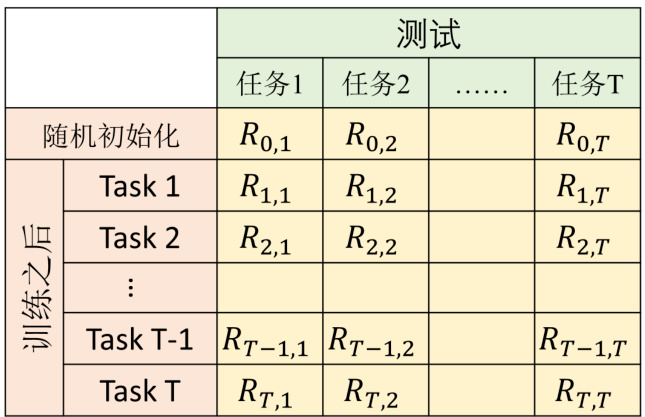
图 16.9 评估终身学习的准确率表格

16.3 终身学习的主要解法

解决终身学习问题，即主要解决灾难性遗忘的问题，通常来讲学术界有几种主要的研究思路。我们首先将第一种主要的解法，即选择性的突触可塑性（selective synaptic plasticity）。顾名思义，就是只让神经网络中的某些神经元之间的连接具有可塑性，其余的必须被固化，这类方法又叫做基于正则的方法。我们可以先回顾一下会什么发生灾难性遗忘这种现象，例如现在有任务一和任务二，并且处于简化考虑，假设训练的模型只有两个参数 ${\theta }_1$ 和 ${\theta }_2$ 。如图 16.10 所示，分别表示了模型在不同任务上的损失函数，如果颜色越偏蓝色，代表损失越小，反之越大。

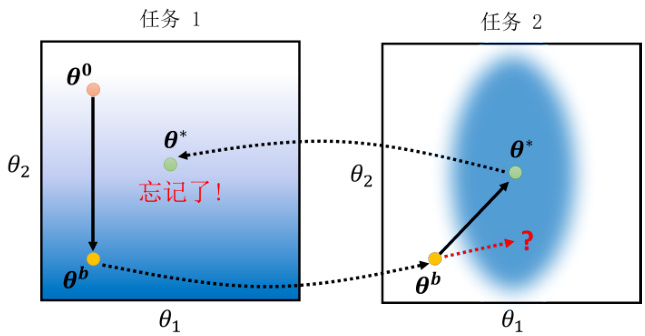
图 16.10 灾难性遗忘示意图

我们先让模型训练任务一，比如给一个随机化的初始参数 ${\theta }^0$ ，用梯度下降的方法更新足够多次数的参数后得到 ${\theta }^b$ 。接下来继续训练任务二，我们先把 ${\theta }^b$ 复制过来放到任务二上，那么由于任务二的损失截面是不同的，即蓝色的区域不同，通过多次迭代我们可能会把参数更新到 ${\theta }^{\ast }$ 的位置。然后我们把在任务二上训练好的参数 ${\theta }^{\ast }$ 拿回到任务一上使用时，会发现并没有办法得到好的结果。因为这个 ${\theta }^{\ast }$ 只是在任务二上表现较好，而不见得会在任务一上有较低的损失和好的表现，这就是灾难性遗忘产生的原因。

那怎么解决这个问题呢？其实对于一个任务而言，要实现较低的损失是可能有很多种不同的参数组合的，比如在任务二中可能所有椭圆内的参数都能有好的表现，而对于任务一则是偏下方的位置都能实现较低的损失。那么如果在跑完任务一之后在训练任务二时，我们的参数不是像右上角移动形成 ${\theta }^{\ast }$ ，而是只往右移动，让最终得到的参数同时处于任务一和任务二较低的损失区域，这种情况下是有可能不会产生灾难性遗忘的。对于这种方式，基本的思想就是每一个参数对我们过去学过的任务的重要性程度是不同的，因此在学习新的任务时，我们尽量不要动那些对过去任务很重要的参数，而是去学一些其他的对新任务比较重要的参数。假设 ${\theta }^b$ 是前一个任务学出来的参数，在选择性的突触可塑性这一解法中会给每一个参数 ${\theta }_i^b$ 赋予一个系数 $b_i$ ，这个系数代表着对应的参数对过去的任务到底重不重要，也称作“守卫”。因此在更新参数的时候，会改写损失函数，如下：

$$L^{\prime }(\theta \theta )=L(\theta \theta )+\lambda \sum _i{b}_i{({\theta }_i-{\theta }_i^b)}^2$$

原来的损失函数写成 $L(\theta )$ ，在学习新任务时不会直接去最小化这个损失函数，否则就会发生灾难性遗忘的问题。我们会在右边一项增加一个当前参数 ${\theta }_i$ 与之前对应的参数 ${\theta }_i^b$ 的平均差并乘上我们讲的重要性系数 $b_i$ 。这里 $b_i=0$ 时，表示我们并不关心学习新任务时的参数需要跟过去的参数有什么联系，即一般的训练，这种情况下就容易发生遗忘。另一种极端就是当 $b_i$ 趋近于无穷大时，即模型参数不肯在新任务上发生妥协，此时可能不会忘记旧的任务，但是也很有可能学不好新的任务，这种情况我们称作不妥协。

接下来比较关键的是 $b_i$ 要怎么设定的问题，也就是某个参数 $b_i$ 到底对任务的重要性有多少。其实有一种简单的控制变量的方法，就是移动或改变某个参数，如图 16.11 所示，我们移动 ${\theta }_1^b$ 时会发现在一定范围内损失值都是很小的，即接近最优的参数，那么我们就可以认为这个参数在一定范围可变，相应的重要性参数 $b_1$ 就可以很小，即这个参数对旧任务来说不是很重要，反之像 ${\theta }_2^b$ 这种不能随意移动的参数对应的重要性参数就必须很大。

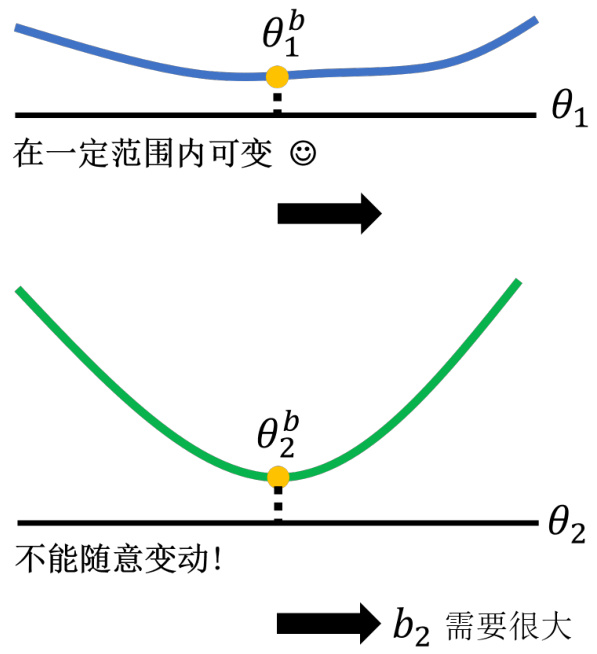
图 16.11 重要性参数设定示例

当然随着后续研究的深入， $b_i$ 的设定也会有各种各样的方法，感兴趣的读者可以了解相关论文，这里就不一一讲解了。

其实在基于正则的方法出现之前，还有一类方法，叫做梯度回合记忆（gradient episodicmemory，MMD），它不是在参数上做限制，而是在梯度更新的方向上做限制，因此又被称为基于梯度的方法。原理如图 16.12 所示，它在计算当前任务梯度方向的同时，也会回去算历史任务对应的梯度方向，然后把两个梯度进行向量求和，得出实际的梯度方向，这样持续更新就能尽可能接近一个不会陷入灾难性遗忘的最优解了。当然新的梯度方向需要满足大于等于

0 的条件，否则很难朝最优解方向优化。

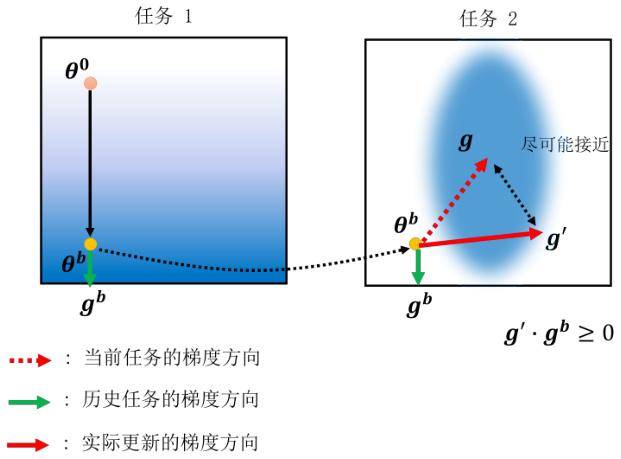
图 16.12 GEM 方法示例

但是这类方法需要把过去的数据同时存储下来，其实这跟终身学习的初衷有些违背了，因为终身学习本身就是希望不需要依赖过去的数据。但由于这里只是存储梯度这些少量的信息，像前面讲的选择性的突触可塑性方法也需要存储一些历史模型信息，所以在实际操作过程中也还能接受。