Support Vector Machine
支持向量机(SVM)有两个特点:SVM=铰链损失(Hinge Loss)+核技巧(Kernel Method)
注:建议先看这篇博客了解SVM基础知识后再看本文的分析
Hinge Loss
Binary Classification
先回顾一下二元分类的做法,为了方便后续推导,这里定义data的标签为-1和+1
当
时, ,表示属于第一类别;当 时, ,表示属于第二类别 原本用
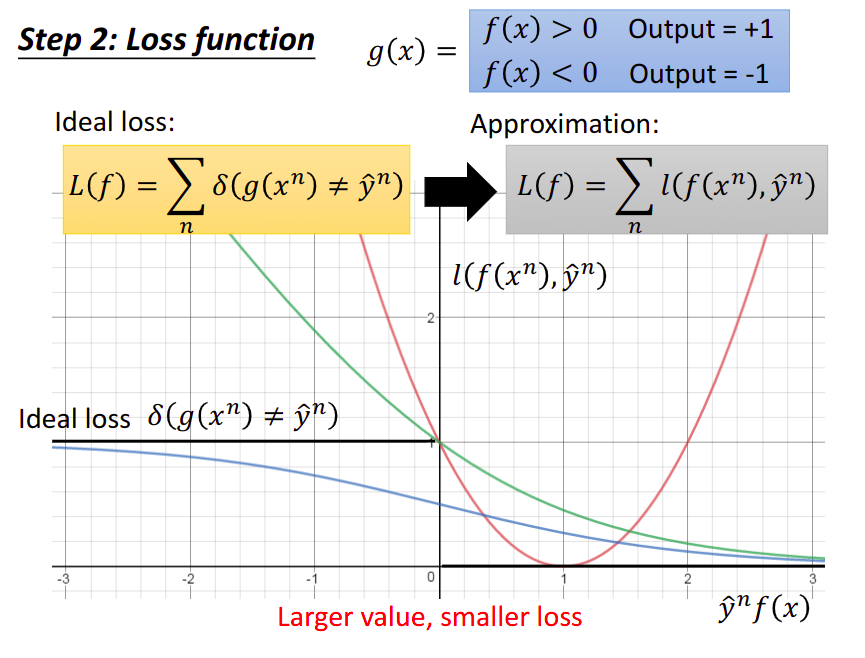
,不匹配的样本点个数,来描述loss function,其中 表示 与 相匹配,反之 ,但这个式子不可微分,无法使用梯度下降法更新参数 因此使用近似的可微分的
来表示损失函数

下图中,横坐标为
- 当
时,希望 越正越好 - 当
时,希望 越负越好
纵坐标是loss,原则上,当横坐标
ideal loss
在
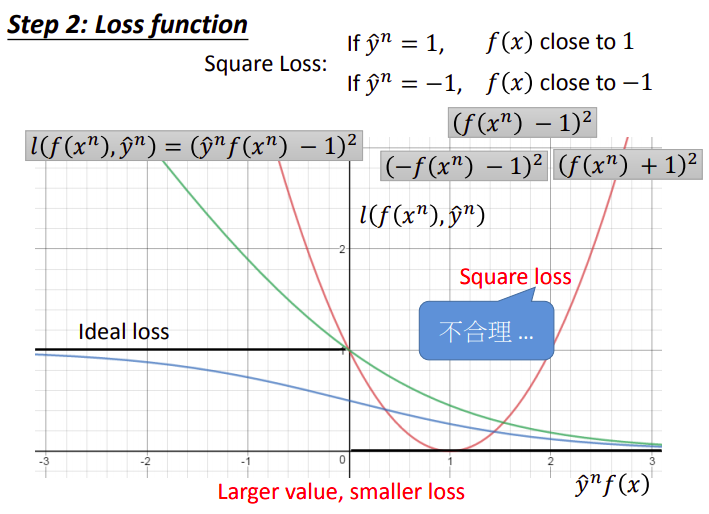
square loss
下图中的红色曲线代表了square loss的损失函数:
- 当
时, 与1越接近越好,此时损失函数化简为 - 当
时, 与-1越接近越好,此时损失函数化简为 - 但实际上整条曲线是不合理的,它会使得
很大的时候有一个更大的loss
sigmoid+square loss
此外蓝线代表sigmoid+square loss的损失函数:
- 当
时, 与1越接近越好,此时损失函数化简为 - 当
时, 与0越接近越好,此时损失函数化简为 - 在逻辑回归的时候实践过,一般square loss的方法表现并不好,而是用cross entropy会更好
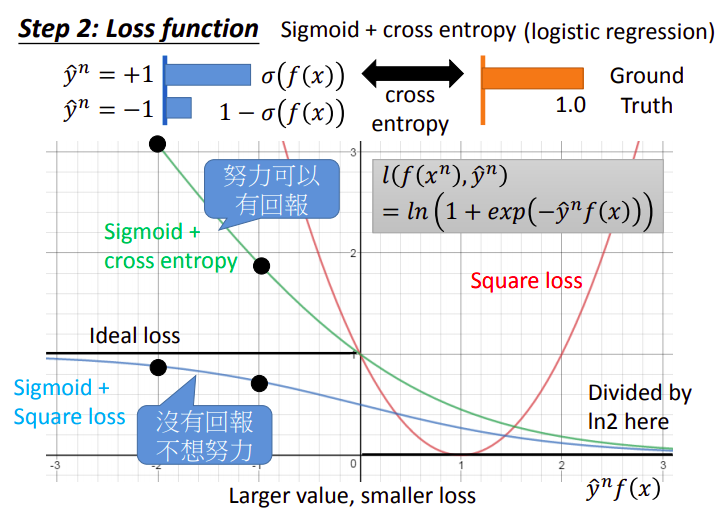
sigmoid+cross entropy
绿线则是代表了sigmoid+cross entropy的损失函数:
代表了一个分布,而Ground Truth则是真实分布,这两个分布之间的交叉熵,就是我们要去minimize的loss - 当
很大的时候,loss接近于0 - 当
很小的时候,loss特别大 - 下图是把损失函数除以
的曲线,使之变成ideal loss的upper bound,且不会对损失函数本身产生影响 - 我们虽然不能minimize理想的loss曲线,但我们可以minimize它的upper bound,从而起到最小化loss的效果
cross entropy VS square error
为什么cross entropy要比square error要来的有效呢?
我们期望在极端情况下,比如
与 非常不匹配导致横坐标非常负的时候,loss的梯度要很大,这样才能尽快地通过参数调整回到loss低的地方 对sigmoid+square loss来说,当横坐标非常负的时候,loss的曲线反而是平缓的,此时去调整参数值对最终loss的影响其实并不大,它并不能很快地降低
形象来说就是,“没有回报,不想努力”
而对cross entropy来说,当横坐标非常负的时候,loss的梯度很大,稍微调整参数就可以往loss小的地方走很大一段距离,这对训练是友好的
形象来说就是,“努力可以有回报""
Hinge Loss
紫线代表了hinge loss的损失函数:
- 当
,损失函数化简为 - 此时只要
,loss就会等于0
- 此时只要
- 当
,损失函数化简为 - 此时只要
,loss就会等于0
- 此时只要
- 总结一下,如果label为1,则当
,机器就认为loss为0;如果label为-1,则当 ,机器就认为loss为0,因此该函数并不需要 有一个很大的值

在紫线中,当
事实上,Hinge Loss也是Ideal loss的upper bound,但是当横坐标
比较Hinge loss和cross entropy,最大的区别在于他们对待已经做得好的样本点的态度,在横坐标
在实作上,两者差距并不大,而Hinge loss的优势在于它不怕outlier,训练出来的结果鲁棒性(robust)比较强
Linear SVM
model description
在线性的SVM里,我们把
在损失函数中,我们通常会加上一个正规项,即
这是一个convex的损失函数,好处在于无论从哪个地方开始做梯度下降,最终得到的结果都会在最低处,曲线中一些折角处等不可微的点可以参考NN中relu、maxout等函数的微分处理
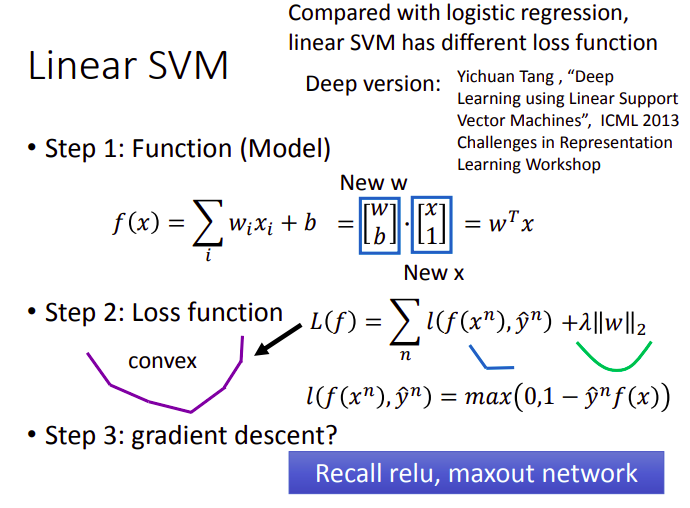
对比Logistic Regression和Linear SVM,两者唯一的区别就是损失函数不同,前者用的是cross entropy,后者用的是Hinge loss
事实上,SVM并不局限于Linear,尽管Linear可以带来很多好的特质,但我们完全可以在一个Deep的神经网络中使用Hinge loss的损失函数,就成为了Deep SVM,其实Deep Learning、SVM这些方法背后的精神都是相通的,并没有那么大的界限
gradient descent
尽管SVM大多不是用梯度下降训练的,但使用该方法训练确实是可行的,推导过程如下:

another formulation
前面列出的式子可能与你平常看到的SVM不大一样,这里将其做一下简单的转换
对
其中
对
但是当加上取loss function

此时该表达式就和你熟知的SVM一样了:
这是一个QP问题(Quadradic programming problem),可以用对应方法求解,当然前面提到的梯度下降法也可以解
Kernel Method
explain linear combination
你要先说服你自己一件事:实际上我们找出来的可以minimize损失函数的参数,其实就是data的线性组合
你可以通过拉格朗日乘数法去求解前面的式子来验证,这里试图从梯度下降的角度来解释:
观察
而使用Hinge loss的时候,

SVM解出来的
redefine model and loss function
知道
这里的
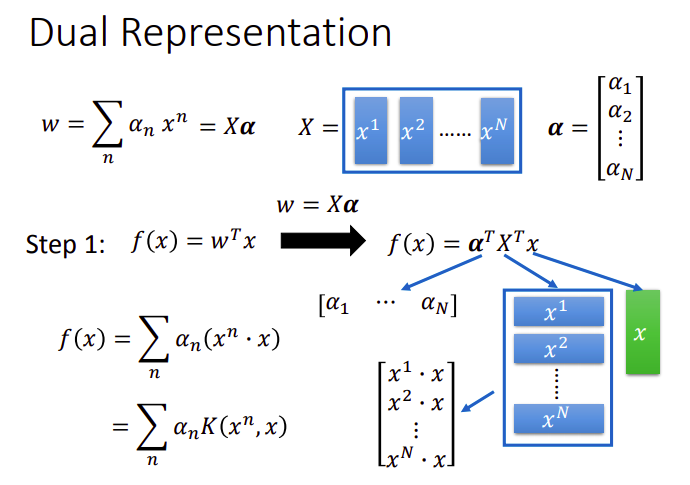
接下来把
此时model就变成了
现在我们的目标是,找一组最好的
从中可以看出,我们并不需要真的知道

Kernel Trick
linear model会有很多的限制,有时候需要对输入的feature做一些转换之后,才能用linear model来处理,假设现在我们的data是二维的,
如果要考虑特征之间的关系,则把特征转换为
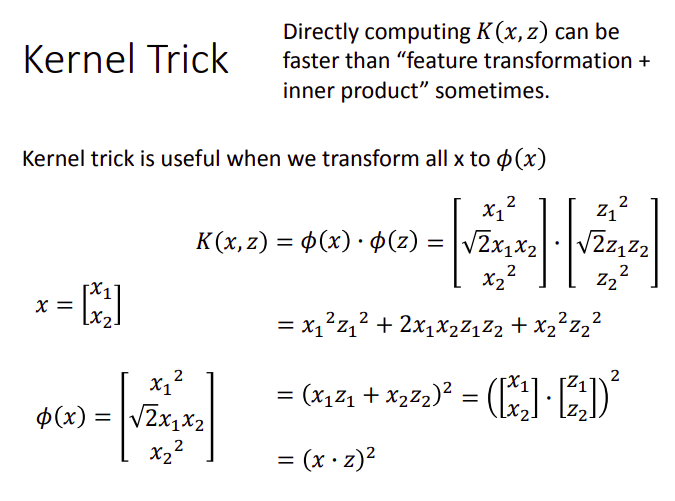
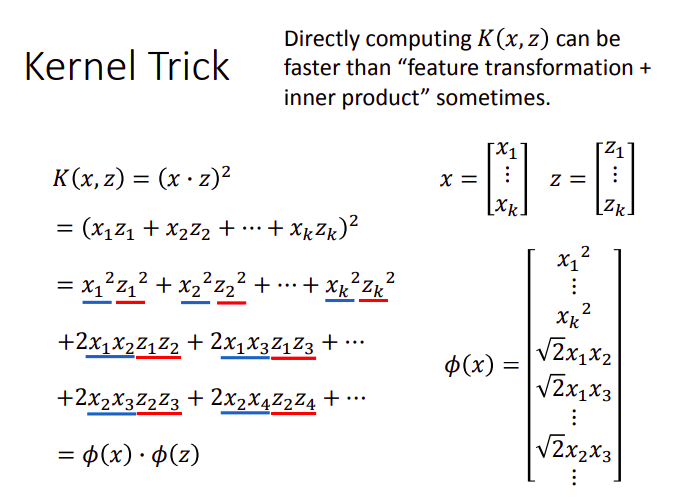
可见,我们对
RBF Kernel
在RBF Kernel中,
将Kernel展开成无穷维如下:

把与
Sigmoid Kernel
Sigmoid Kernel:
如果使用的是Sigmoid Kernel,那model
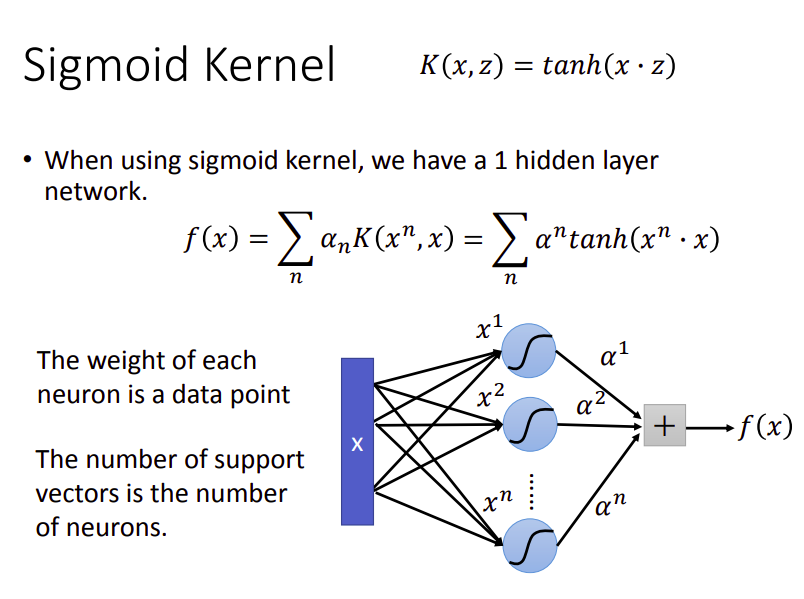
其中neuron的数目,由support vector的数量决定
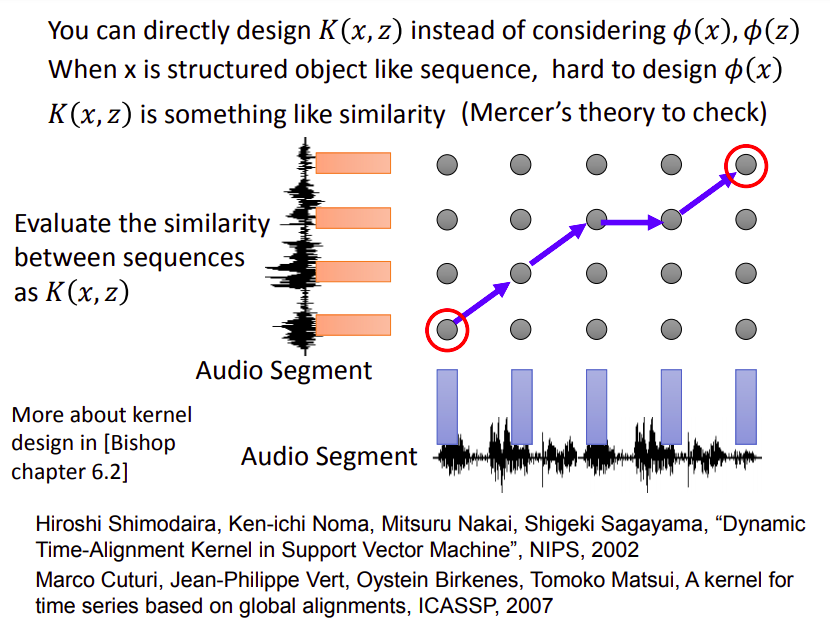
Design Kernel Function
既然有了Kernel Trick,其实就可以直接去设计Kernel Function,它代表了投影到高维以后的内积,类似于相似度的概念
我们完全可以不去管
当
我们随便定义一个Kernel Function,其实并不一定能够拆成两个向量内积的结果,但有Mercer's theory可以帮助你判断当前的function是否可拆分
下图是直接定义语音vector之间的相似度
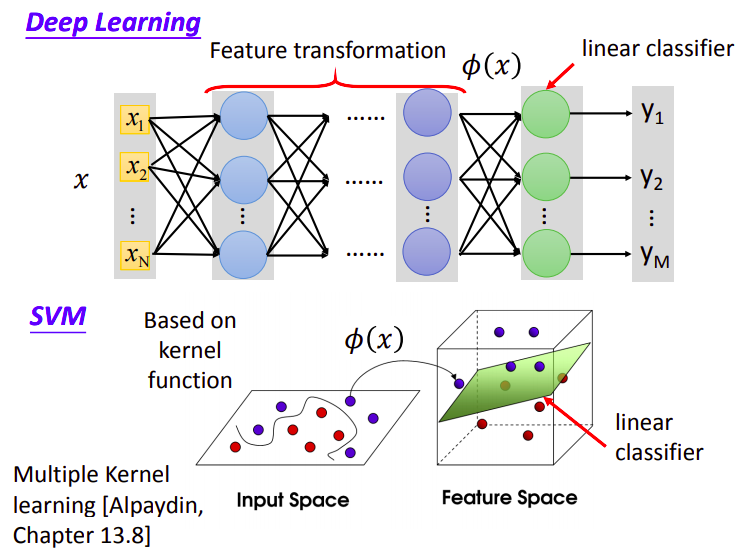
SVM vs Deep Learning
这里简单比较一下SVM和Deep Learning的差别:
deep learning的前几层layer可以看成是在做feature transform,而后几层layer则是在做linear classifier
SVM也类似,先用Kernel Function把feature transform到高维空间上,然后再使用linear classifier
在SVM里一般Linear Classifier都会采用Hinge Loss