Regression:Case Study
回归-案例研究
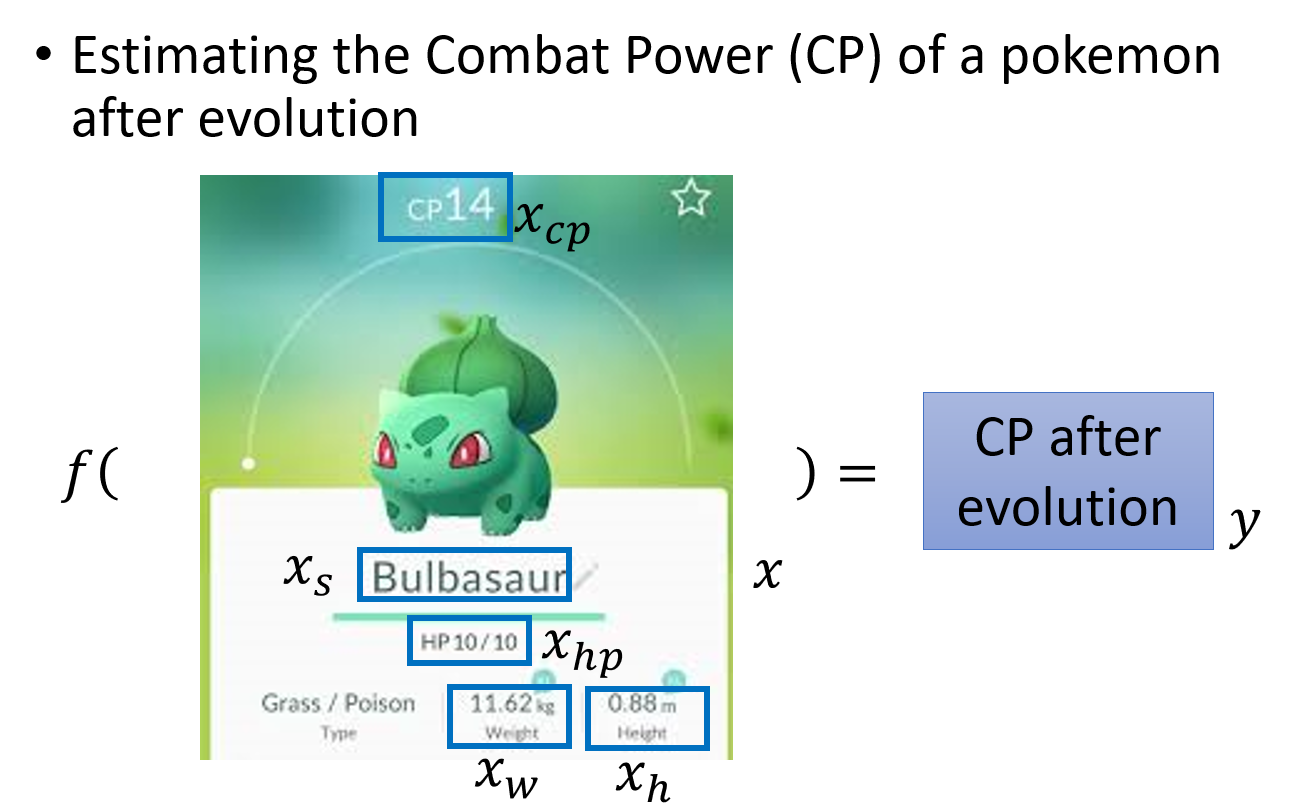
问题的导入:预测宝可梦的CP值
Estimating the Combat Power(CP) of a pokemon after evolution
我们期望根据已有的宝可梦进化前后的信息,来预测某只宝可梦进化后的cp值的大小
确定Senario、Task和Model
Senario
首先根据已有的data来确定Senario,我们拥有宝可梦进化前后cp值的这样一笔数据,input是进化前的宝可梦(包括它的各种属性),output是进化后的宝可梦的cp值;因此我们的data是labeled,使用的Senario是Supervised Learning
Task
然后根据我们想要function的输出类型来确定Task,我们预期得到的是宝可梦进化后的cp值,是一个scalar,因此使用的Task是Regression
Model
关于Model,选择很多,这里采用的是Non-linear Model
设定具体参数
Regression的具体过程
回顾一下machine Learning的三个步骤:
- 定义一个model即function set
- 定义一个goodness of function损失函数去评估该function的好坏
- 找一个最好的function
Step1:Model (function set)
如何选择一个function的模型呢?毕竟只有确定了模型才能调参。这里没有明确的思路,只能凭经验去一种种地试
Linear Model 线性模型
y代表进化后的cp值,
根据不同的w和b,可以确定不同的无穷无尽的function,而
实际上这是一种Linear Model,但只考虑了宝可梦进化前的cp值,因而我们可以将其扩展为:
==
x~i~: an attribute of input X ( x~i~ is also called feature,即特征值)
w~i~:weight of x~i~
b: bias

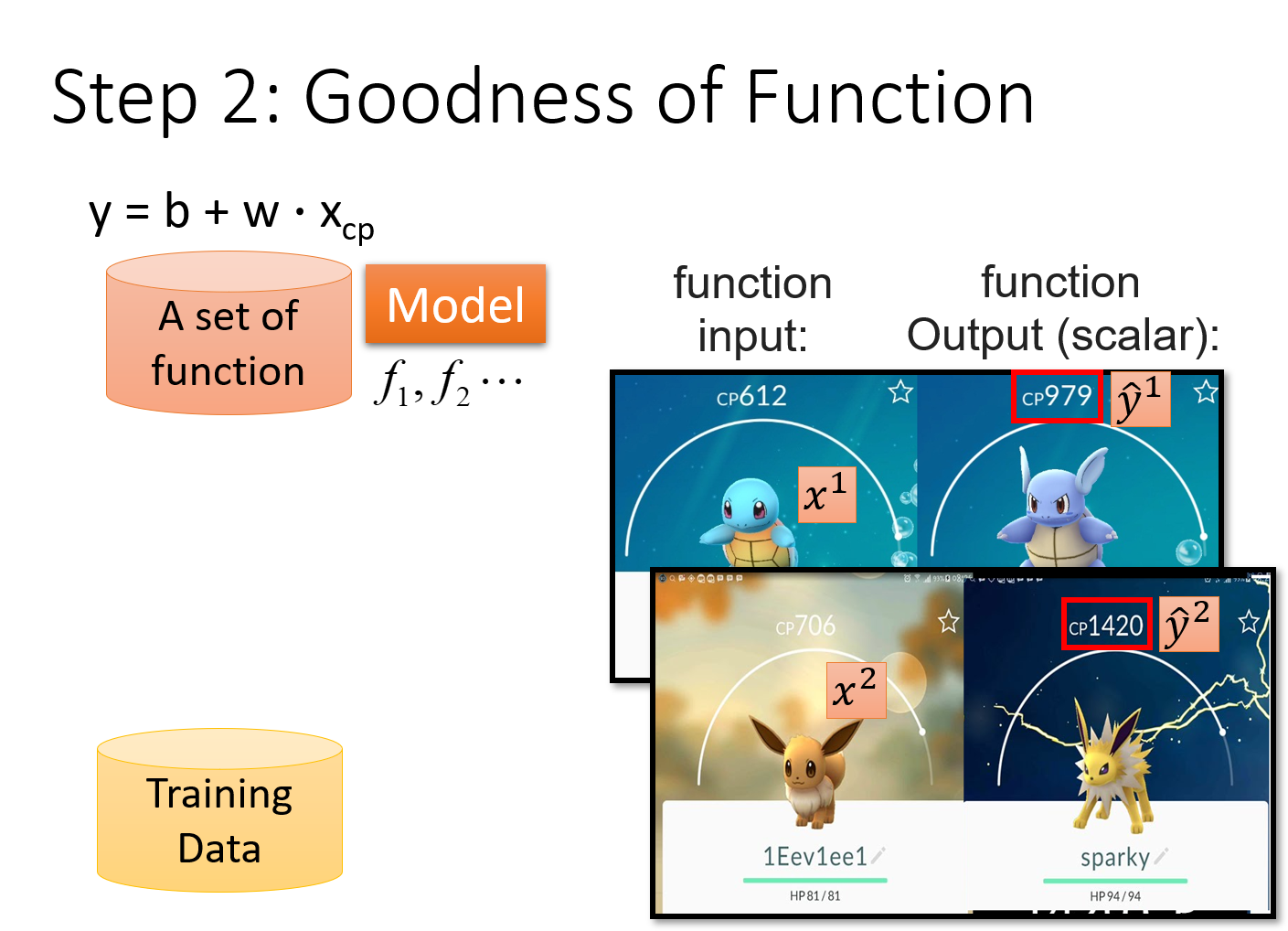
Step2:Goodness of Function
参数说明
注:由于regression的输出值是scalar,因此
Loss function 损失函数
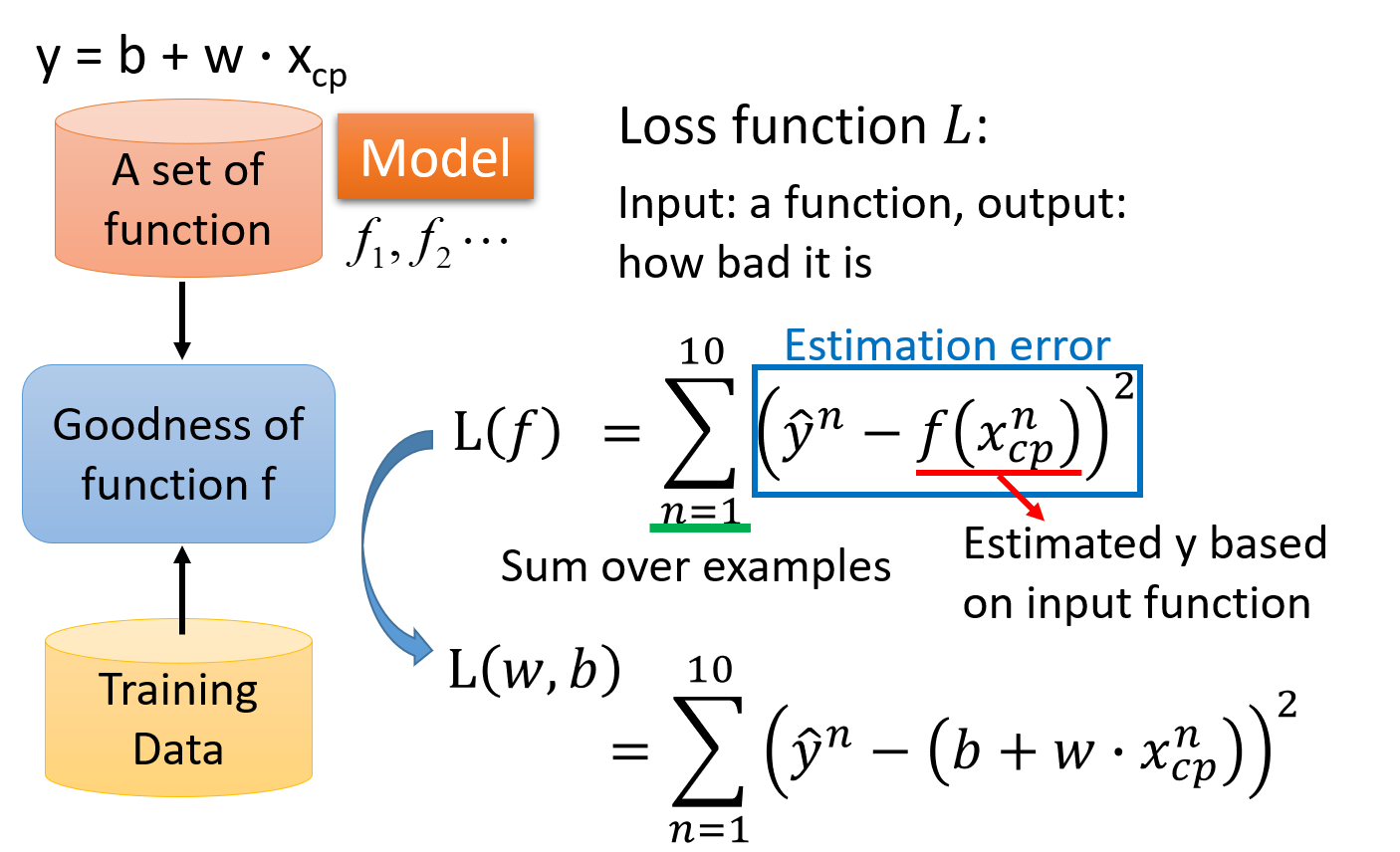
为了衡量function set中的某个function的好坏,我们需要一个评估函数,即==Loss function==,损失函数,简称L;loss function是一个function的function
input:a function;
output:how bad/good it is
由于f是由b和w决定的,因此input f就等价于input这个f里的b和w,因此==Loss function实际上是在衡量一组参数的好坏==
之前提到的model是由我们自主选择的,这里的loss function也是,最常用的方法就是采用类似于方差和的形式来衡量参数的好坏,即预测值与真值差的平方和;这里真正的数值减估测数值的平方,叫做估测误差,Estimation error,将10个估测误差合起来就是loss function
如果
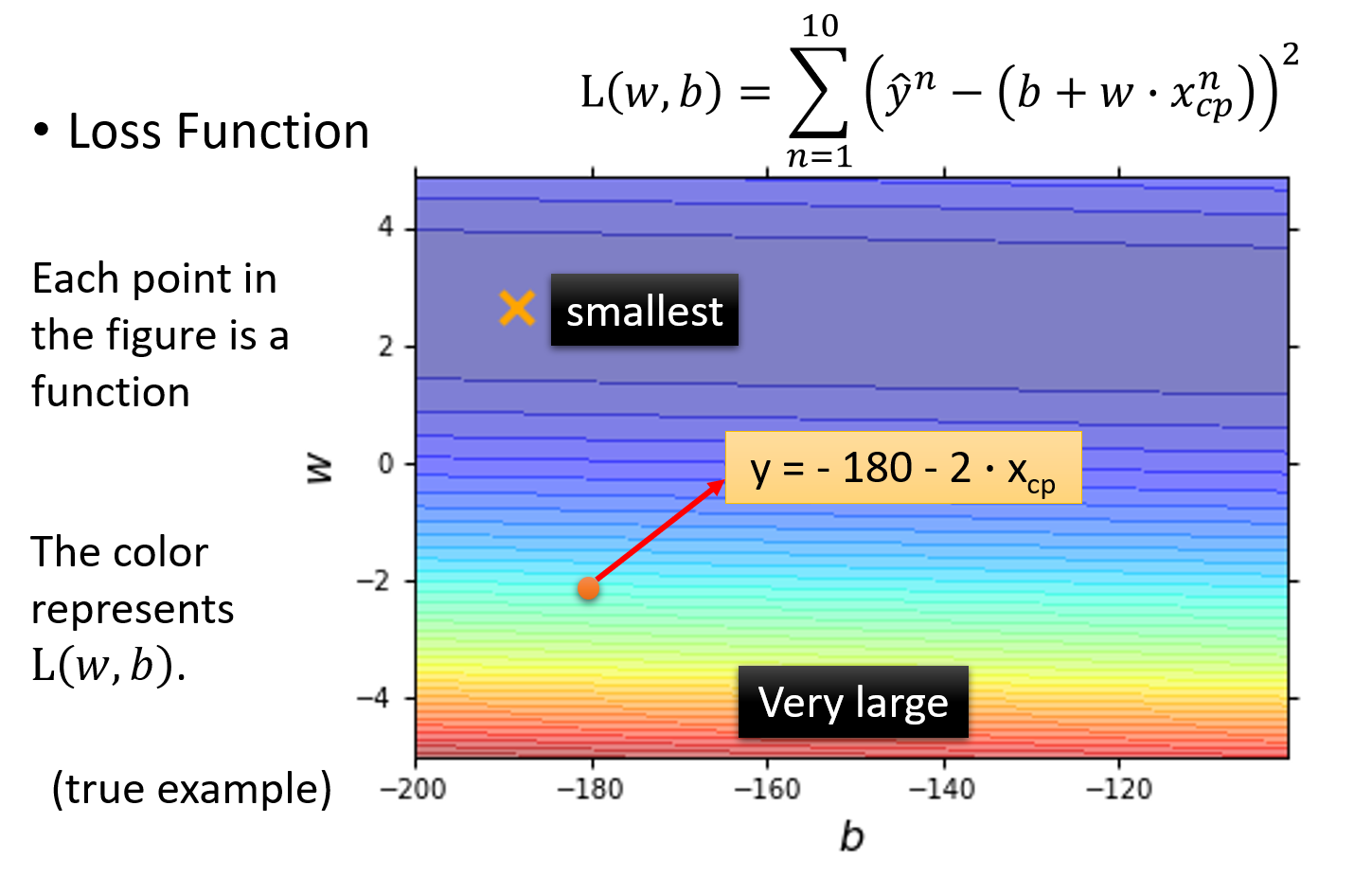
Loss function可视化
下图中是loss function的可视化,该图中的每一个点都代表一组(w,b),也就是对应着一个function;而该点的颜色对应着的loss function的结果L(w,b),它表示该点对应function的表现有多糟糕,颜色越偏红色代表Loss的数值越大,这个function的表现越不好,越偏蓝色代表Loss的数值越小,这个function的表现越好
比如图中用红色箭头标注的点就代表了b=-180 , w=-2对应的function,即
Step3:Pick the Best Function
我们已经确定了loss function,他可以衡量我们的model里面每一个function的好坏,接下来我们要做的事情就是,从这个function set里面,挑选一个最好的function
挑选最好的function这一件事情,写成formulation/equation的样子如下:
也就是那个使
 利用线性代数的知识,可以解得这个closed-form solution,但这里采用的是一种更为普遍的方法——==gradient descent(梯度下降法)==
利用线性代数的知识,可以解得这个closed-form solution,但这里采用的是一种更为普遍的方法——==gradient descent(梯度下降法)==
Gradient Descent 梯度下降
上面的例子比较简单,用线性代数的知识就可以解;但是对于更普遍的问题来说,==gradient descent的厉害之处在于,只要
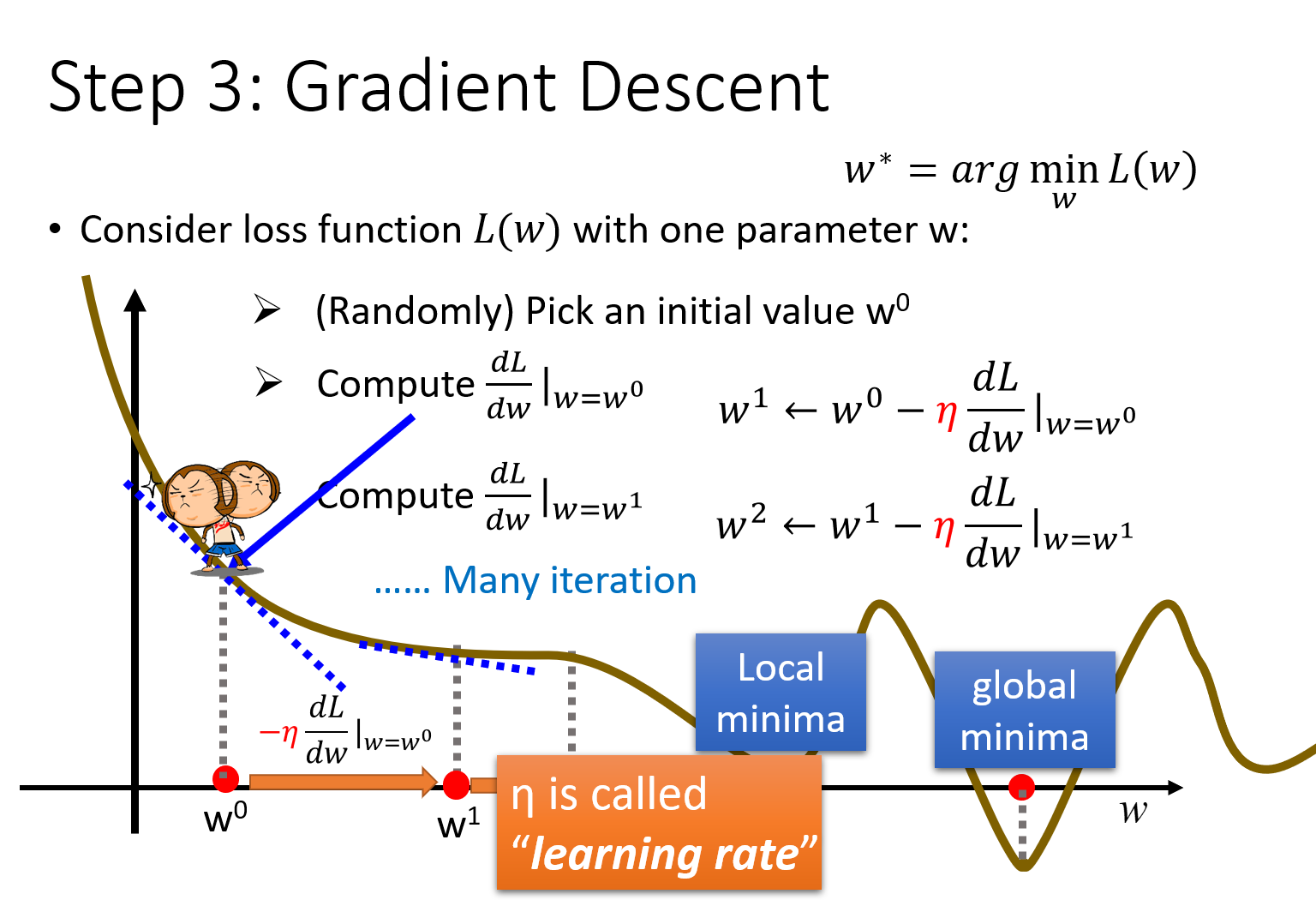
单个参数的问题
以只带单个参数w的Loss Function L(w)为例,首先保证
w^1=w^0-η \frac{dL}{dw}|_{w=w^0} \\
w^2=w^1-η \frac{dL}{dw}|_{w=w^1} \\
w^3=w^2-η \frac{dL}{dw}|_{w=w^2} \\
... \\
w^{i+1}=w^i-η \frac{dL}{dw}|_{w=w^i} \\
if\ \ (\frac{dL}{dw}|_{w=w^i}==0) \ \ then \ \ stop;
$$
此时$w^i$对应的斜率为0,我们找到了一个极小值local minima,这就出现了一个问题,当微分为0的时候,参数就会一直卡在这个点上没有办法再更新了,因此通过gradient descent找出来的solution其实并不是最佳解global minima
但幸运的是,在linear regression上,是没有local minima的,因此可以使用这个方法
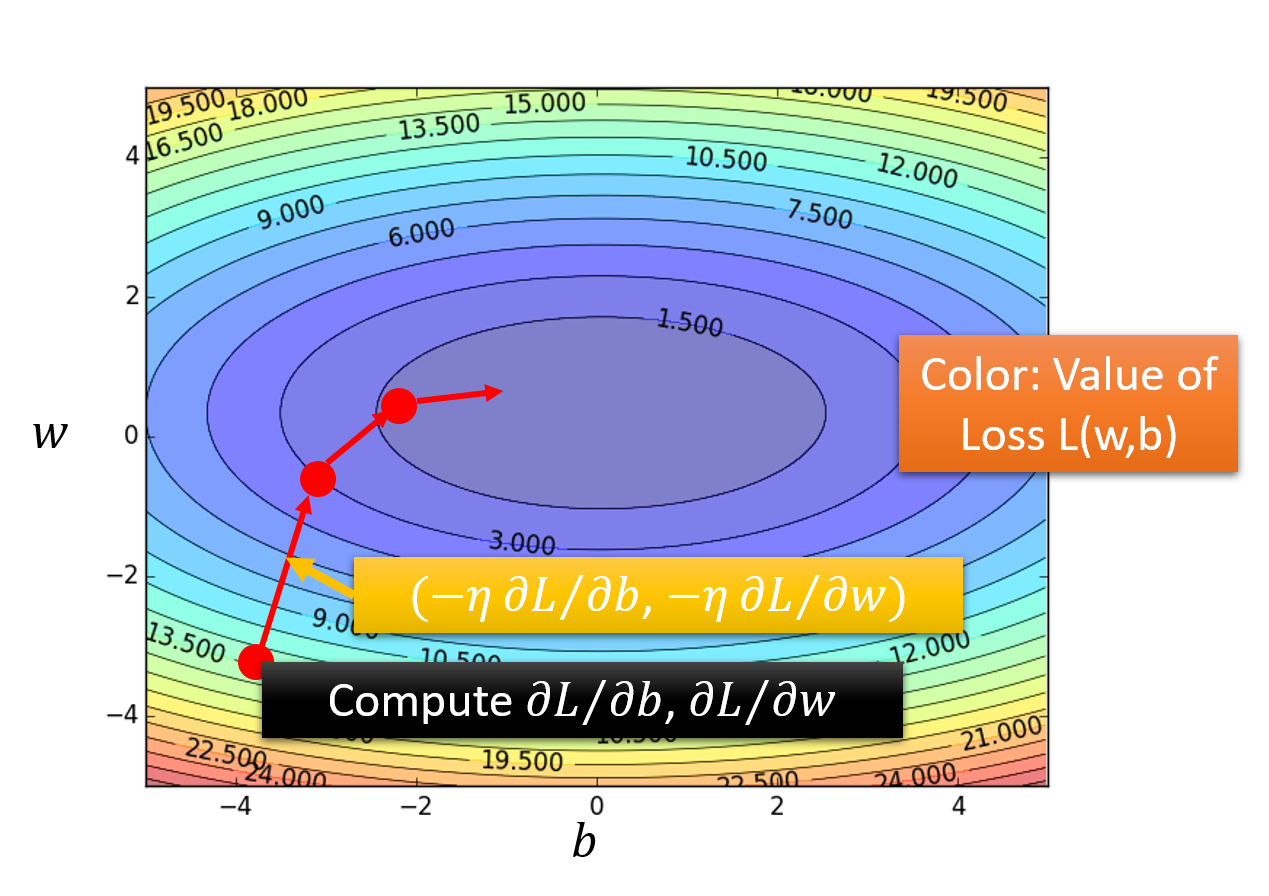
两个参数的问题
今天要解决的关于宝可梦的问题,是含有two parameters的问题,即
当然,它本质上处理单个参数的问题是一样的
首先,也是随机选取两个初始值,
和 然后分别计算
这个点上,L对w和b的偏微分,即 和 更新参数,当迭代跳出时,
对应着极小值点
实际上,L 的gradient就是微积分中的那个梯度的概念,即
可视化效果如下:(三维坐标显示在二维图像中,loss的值用颜色来表示)
横坐标是b,纵坐标是w,颜色代表loss的值,越偏蓝色表示loss越小,越偏红色表示loss越大
每次计算得到的梯度gradient,即由
注:这里两个方向的η(learning rate)必须保持一致,这样每次更新坐标的step size是等比例缩放的,保证坐标前进的方向始终和梯度下降的方向一致;否则坐标前进的方向将会发生偏移
Gradient Descent的缺点
gradient descent有一个令人担心的地方,也就是我之前一直提到的,它每次迭代完毕,寻找到的梯度为0的点必然是极小值点,local minima;却不一定是最小值点,global minima
这会造成一个问题是说,如果loss function长得比较坑坑洼洼(极小值点比较多),而每次初始化
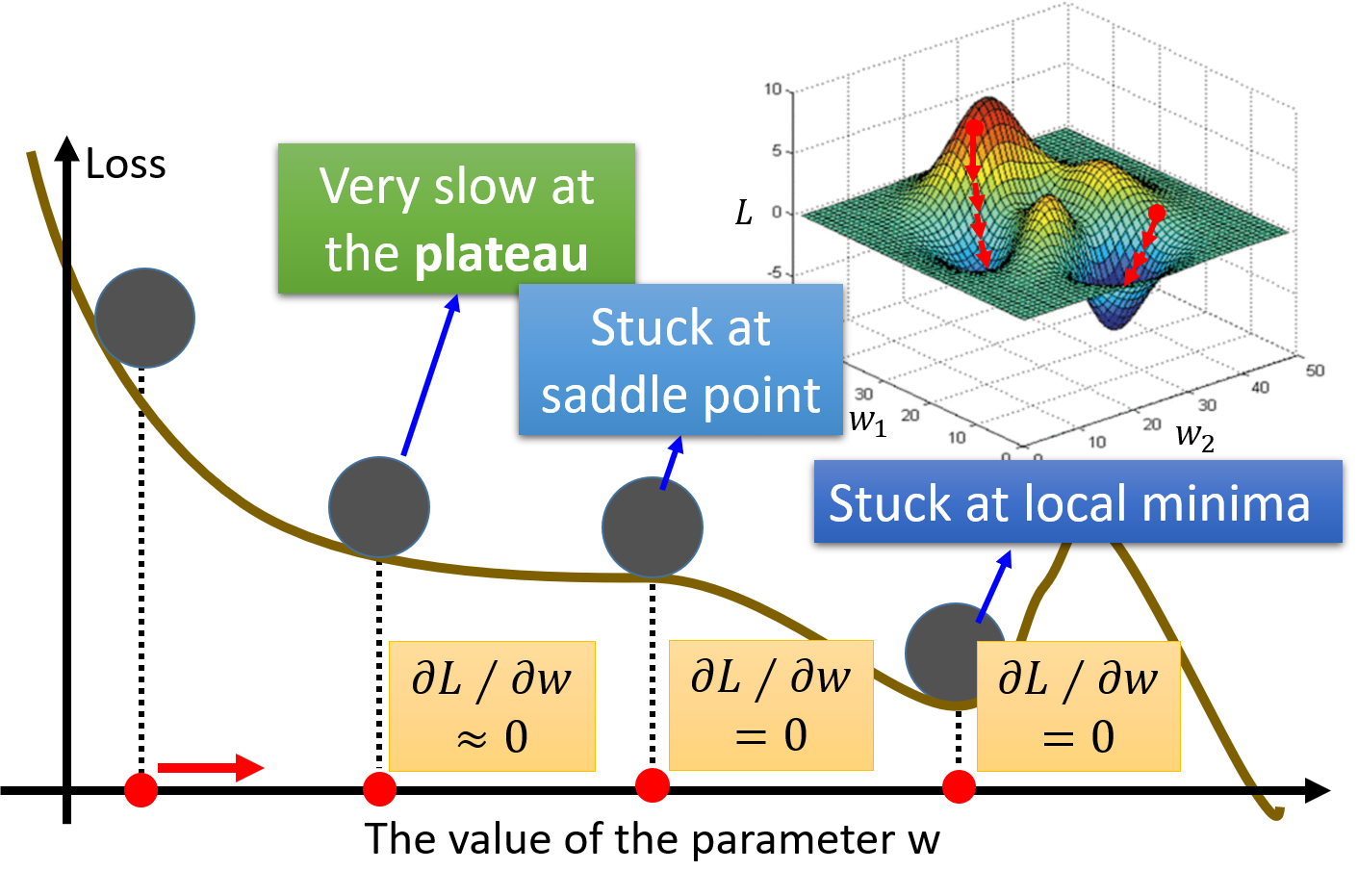 但是!在==linear regression==里,loss function实际上是convex的,是一个凸函数,是没有local optimal局部最优解的,他只有一个global minima,visualize出来的图像就是从里到外一圈一圈包围起来的椭圆形的等高线(就像前面的等高线图),因此随便选一个起始点,根据gradient descent最终找出来的,都会是同一组参数
但是!在==linear regression==里,loss function实际上是convex的,是一个凸函数,是没有local optimal局部最优解的,他只有一个global minima,visualize出来的图像就是从里到外一圈一圈包围起来的椭圆形的等高线(就像前面的等高线图),因此随便选一个起始点,根据gradient descent最终找出来的,都会是同一组参数
回到pokemon的问题上来
偏微分的计算
现在我们来求具体的L对w和b的偏微分
How's the results?
根据gradient descent,我们得到的
我们需要有一套评估系统来评价我们得到的最后这个function和实际值的误差error的大小;这里我们将training data里每一只宝可梦
What we really care about is the error on new data (testing data)
当然我们真正关心的是generalization的case,也就是用这个model去估测新抓到的pokemon,误差会有多少,这也就是所谓的testing data的误差;于是又抓了10只新的pokemon,算出来的Average Error on Testing Data为
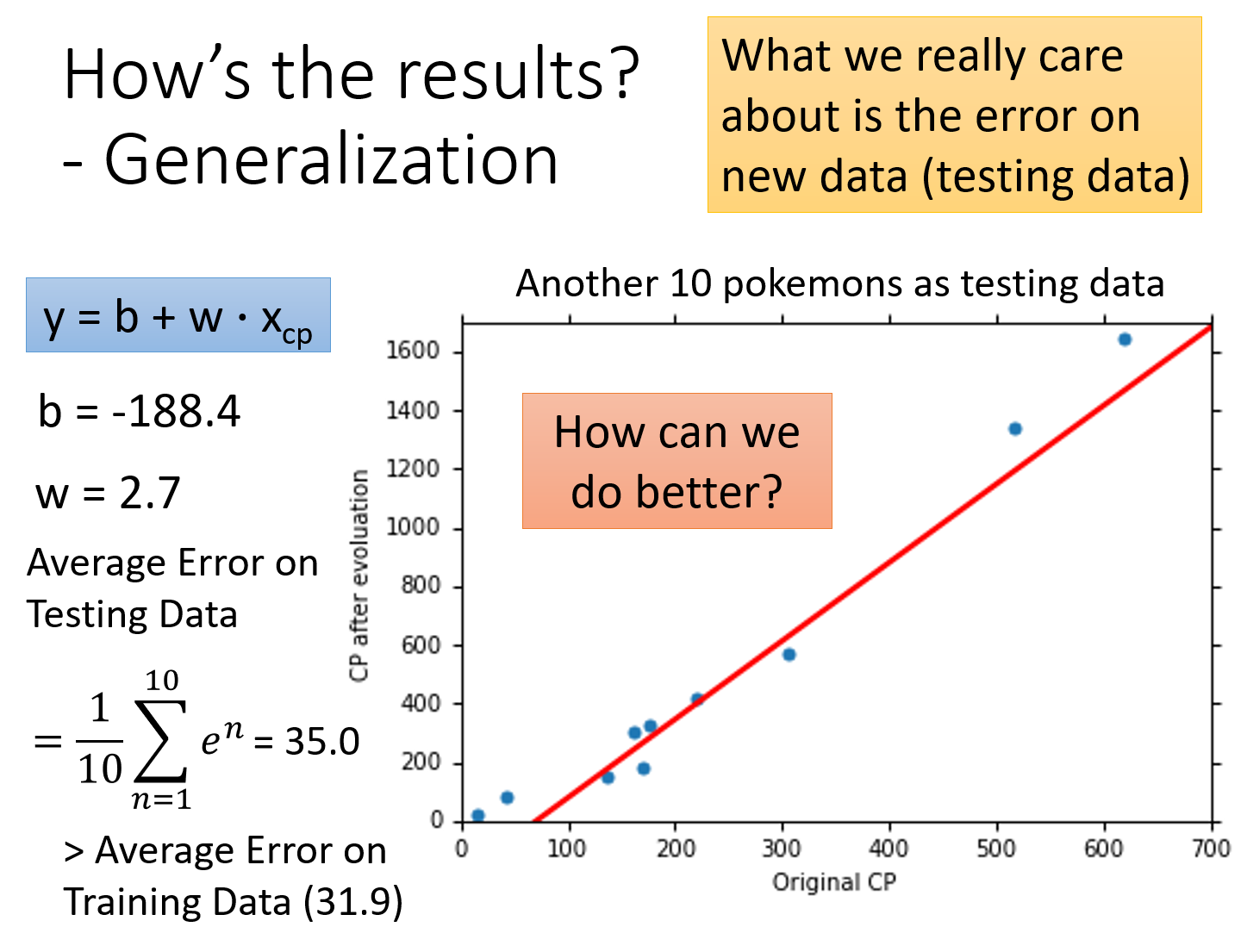
How can we do better?
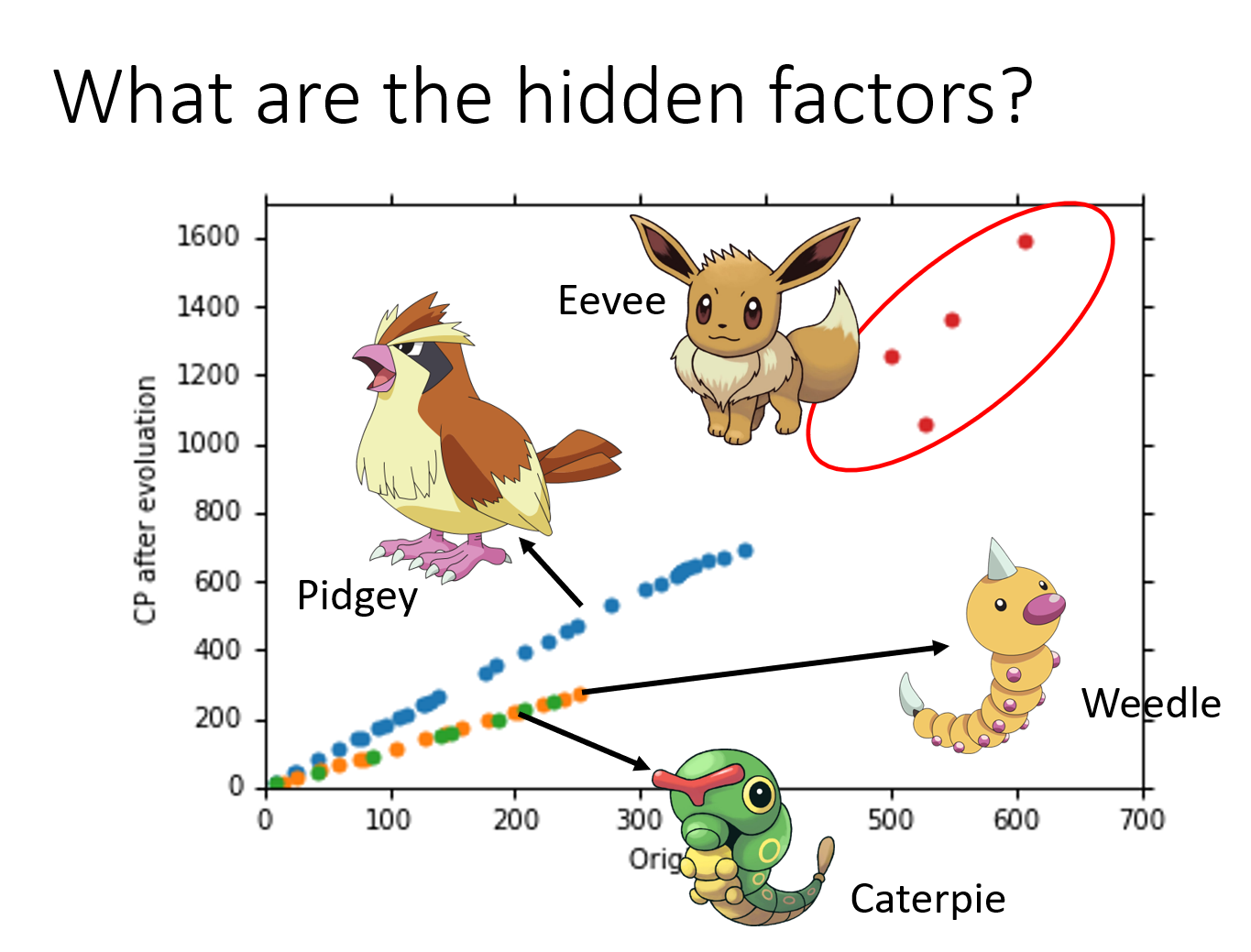
我们有没有办法做得更好呢?这时就需要我们重新去设计model;如果仔细观察一下上图的data,就会发现在原先的cp值比较大和比较小的地方,预测值是相当不准的
实际上,从结果来看,最终的function可能不是一条直线,可能是稍微更复杂一点的曲线
考虑
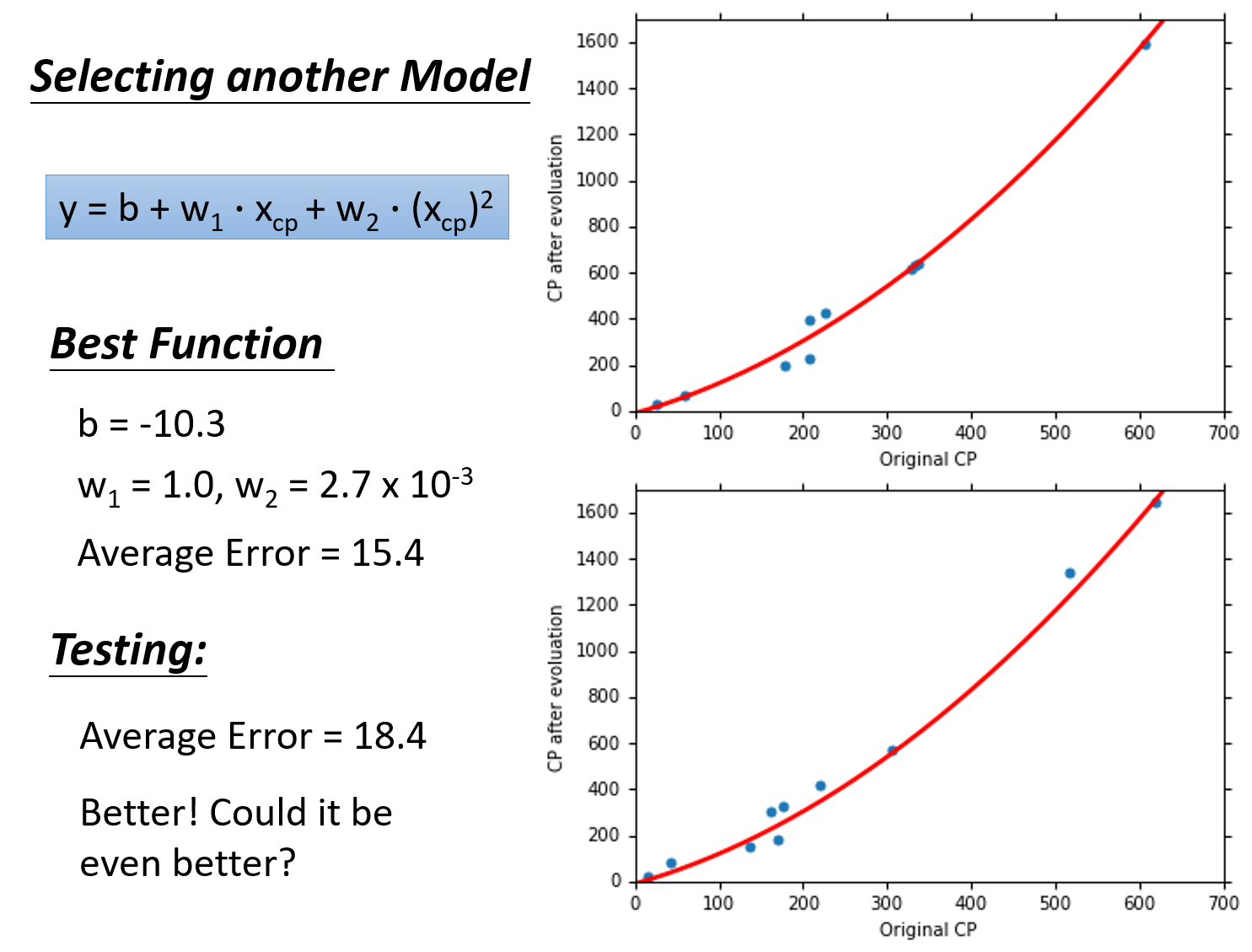
考虑
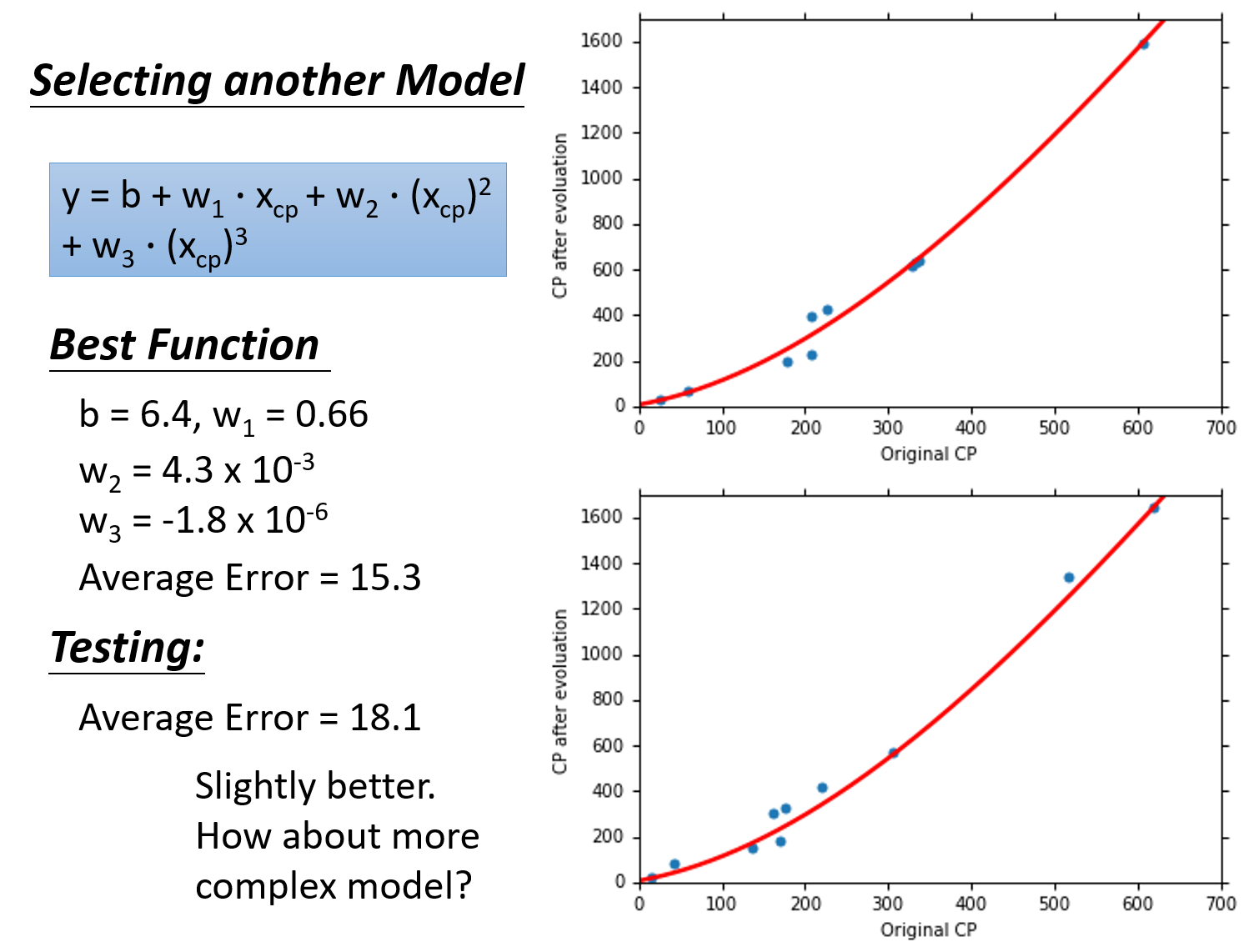
考虑
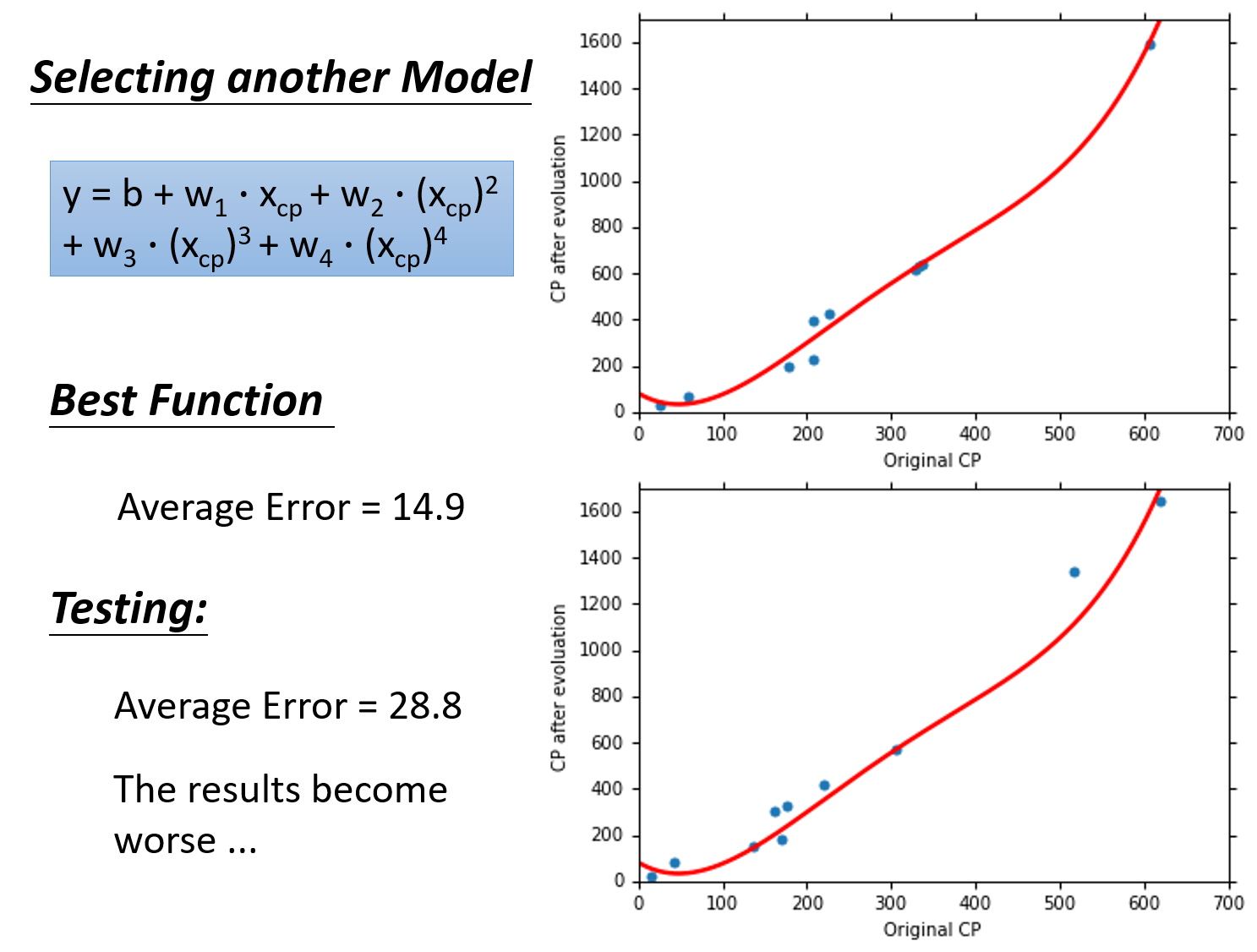
考虑
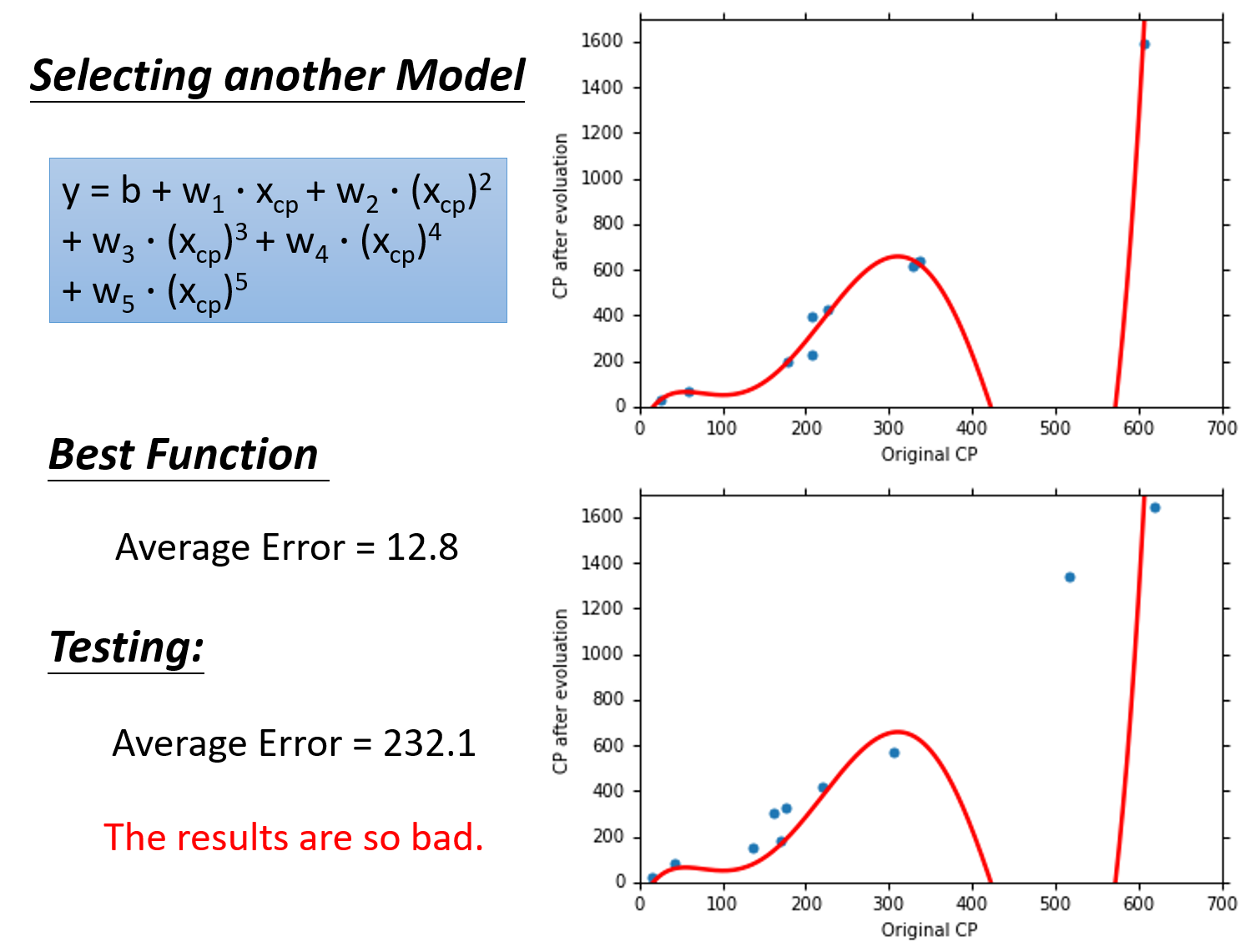
5个model的对比
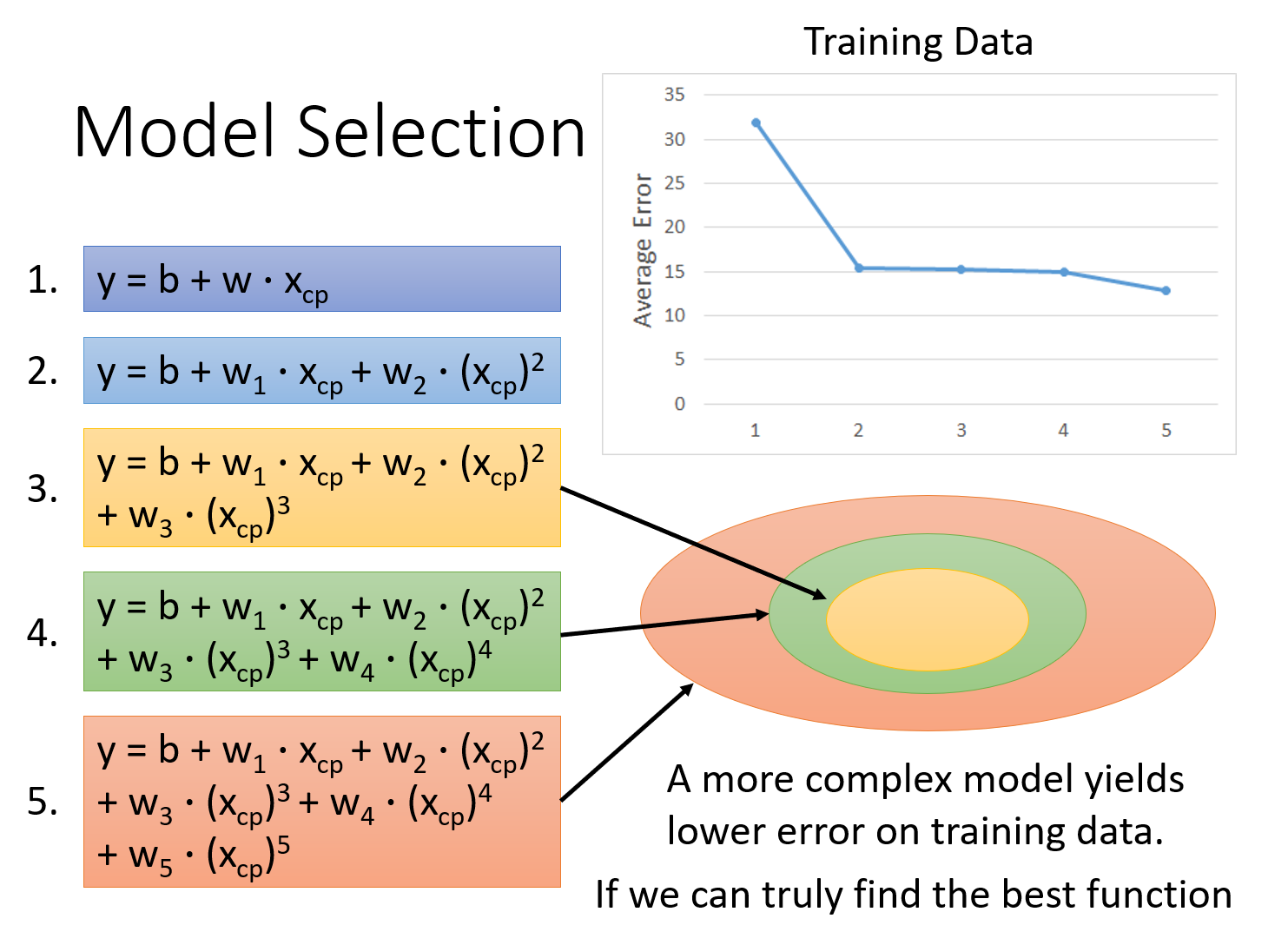
这5个model的training data的表现:随着
也就是说,在gradient descent可以找到best function的前提下(多次式为Non-linear model,存在local optimal局部最优解,gradient descent不一定能找到global minima),function所包含的项的次数越高,越复杂,error在training data上的表现就会越来越小;但是,我们关心的不是model在training data上的error表现,而是model在testing data上的error表现
 在training data上,model越复杂,error就会越低;但是在testing data上,model复杂到一定程度之后,error非但不会减小,反而会暴增,在该例中,从含有
在training data上,model越复杂,error就会越低;但是在testing data上,model复杂到一定程度之后,error非但不会减小,反而会暴增,在该例中,从含有
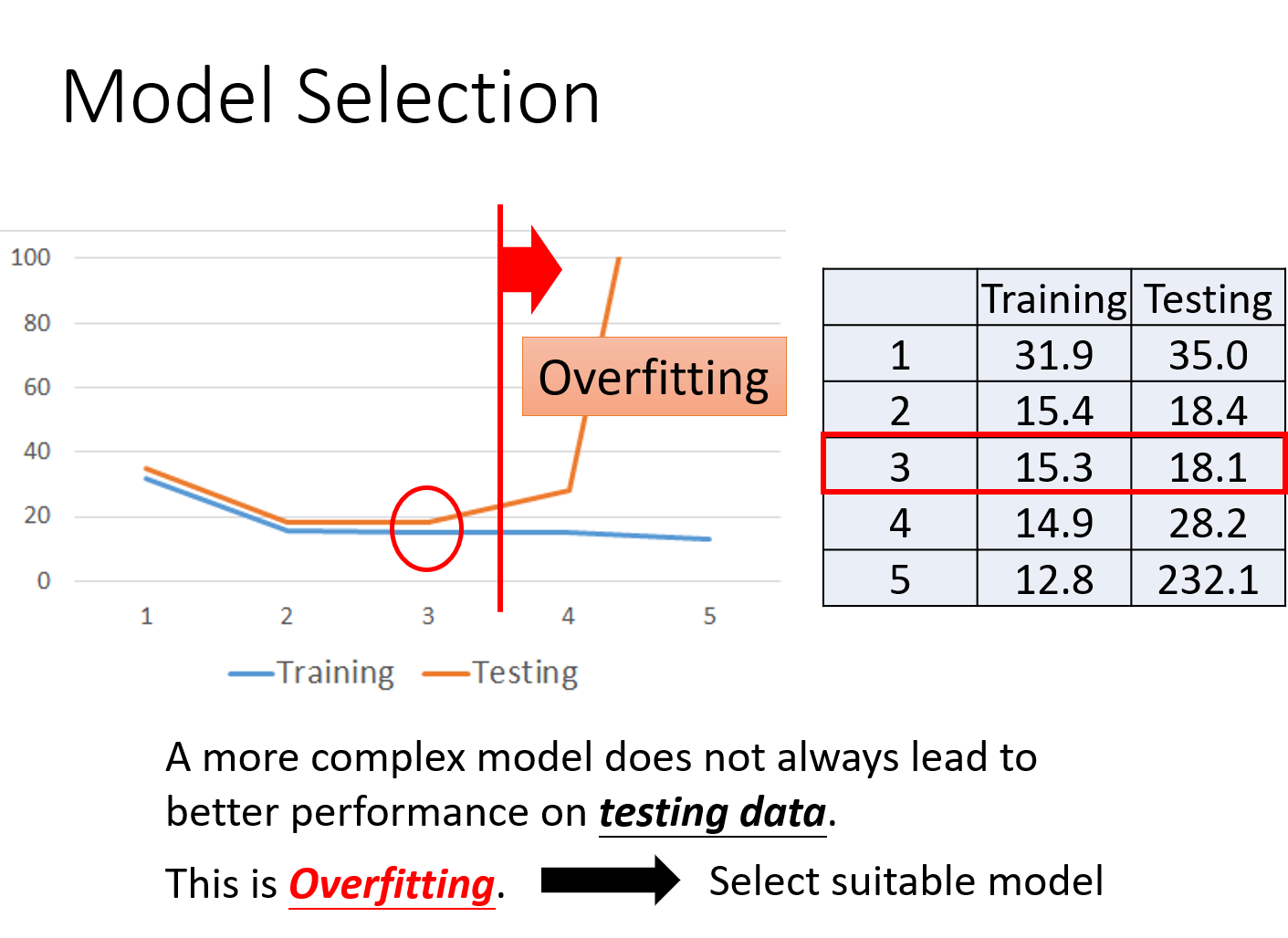 因此model不是越复杂越好,而是选择一个最适合的model,在本例中,包含
因此model不是越复杂越好,而是选择一个最适合的model,在本例中,包含
进一步讨论其他参数
物种
之前我们的model只考虑了宝可梦进化前的cp值,这显然是不对的,除了cp值外,还受到物种
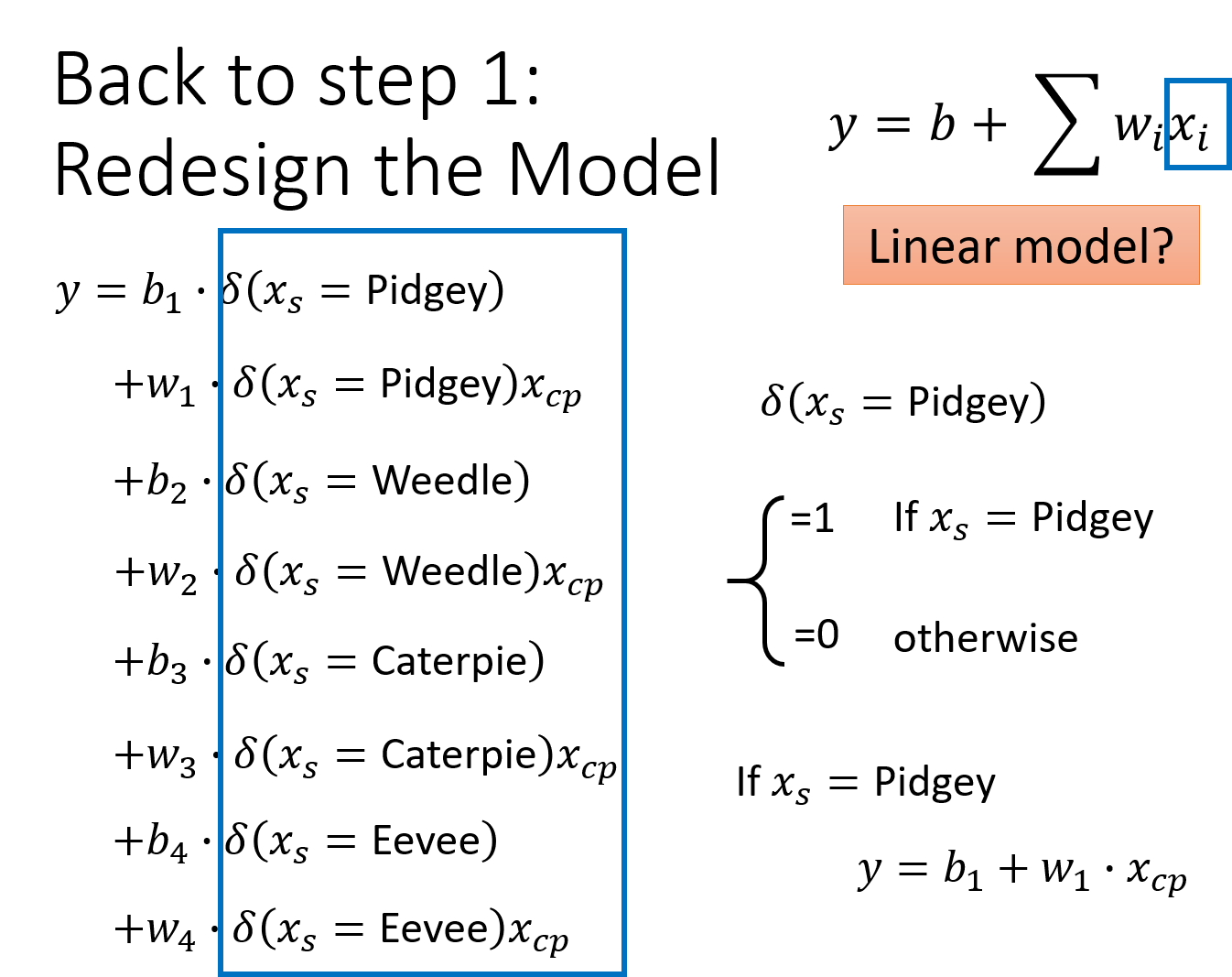
 因此我们重新设计model:
因此我们重新设计model:
也就是根据不同的物种,设计不同的linear model(这里
这里引入
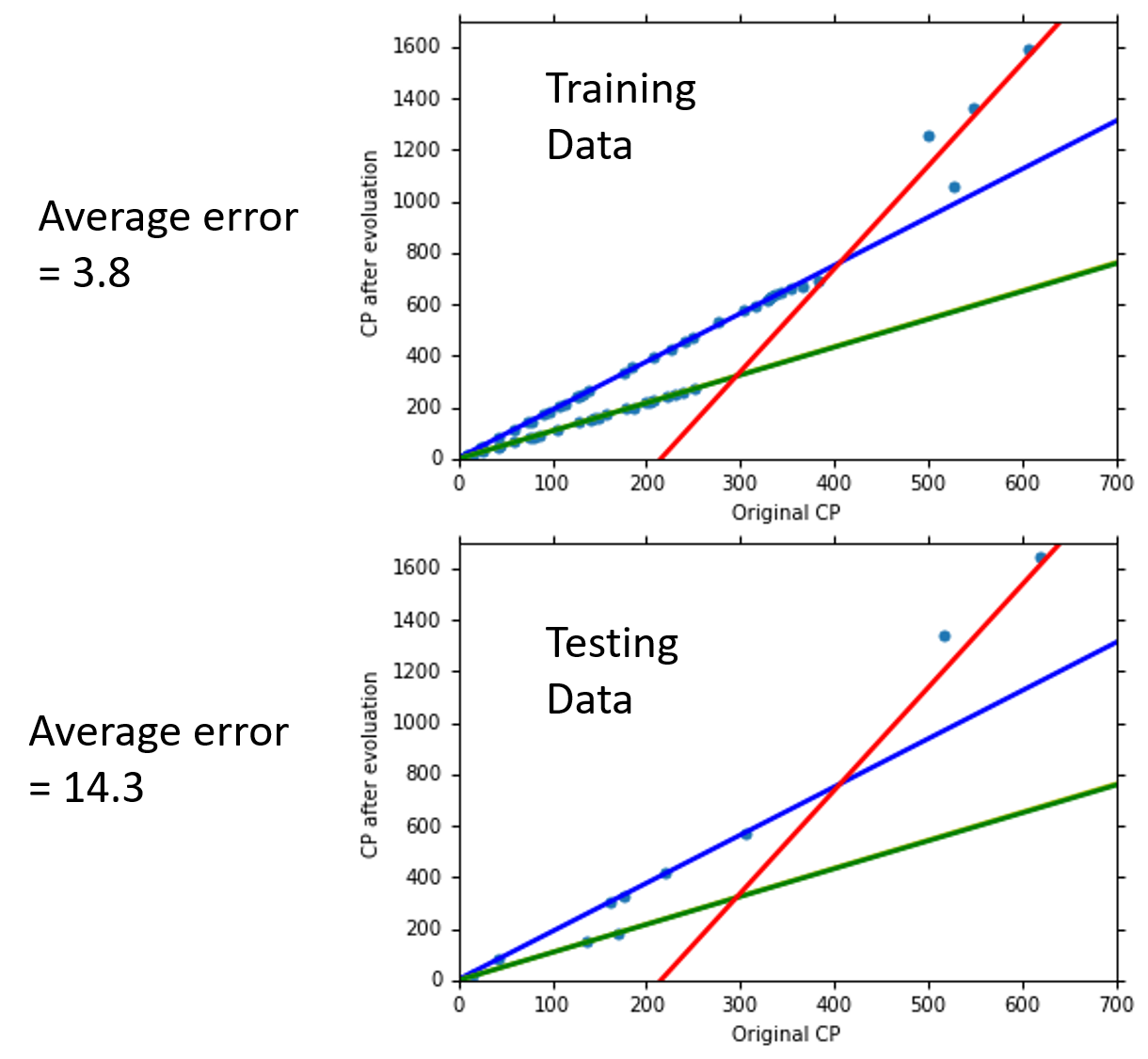
 有了上面这个model以后,我们分别得到了在training data和testing data上测试的结果:
有了上面这个model以后,我们分别得到了在training data和testing data上测试的结果:
Hp值
考虑所有可能有影响的参数,设计出这个最复杂的model:
算出的training error=1.9,但是,testing error=102.3!这么复杂的model很大概率会发生overfitting(按照我的理解,overfitting实际上是我们多使用了一些input的变量或是变量的高次项使曲线跟training data拟合的更好,但不幸的是这些项并不是实际情况下被使用的,于是这个model在testing data上会表现得很糟糕),overfitting就相当于是那个范围更大的韦恩图,它包含了更多的函数更大的范围,代价就是在准确度上表现得更糟糕
regularization解决overfitting(L2正则化解决过拟合问题)
regularization可以使曲线变得更加smooth,training data上的error变大,但是 testing data上的error变小。有关regularization的具体原理说明详见下一部分
原来的loss function只考虑了prediction的error,即
也就是说,我们期待参数
因为参数值接近0的function,是比较平滑的;所谓的平滑的意思是,当今天的输入有变化的时候,output对输入的变化是比较不敏感的
举例来说,对
那为什么我们喜欢比较平滑的function呢?
如果我们有一个比较平滑的function,由于输出对输入是不敏感的,测试的时候,一些noises噪声对这个平滑的function的影响就会比较小,而给我们一个比较好的结果
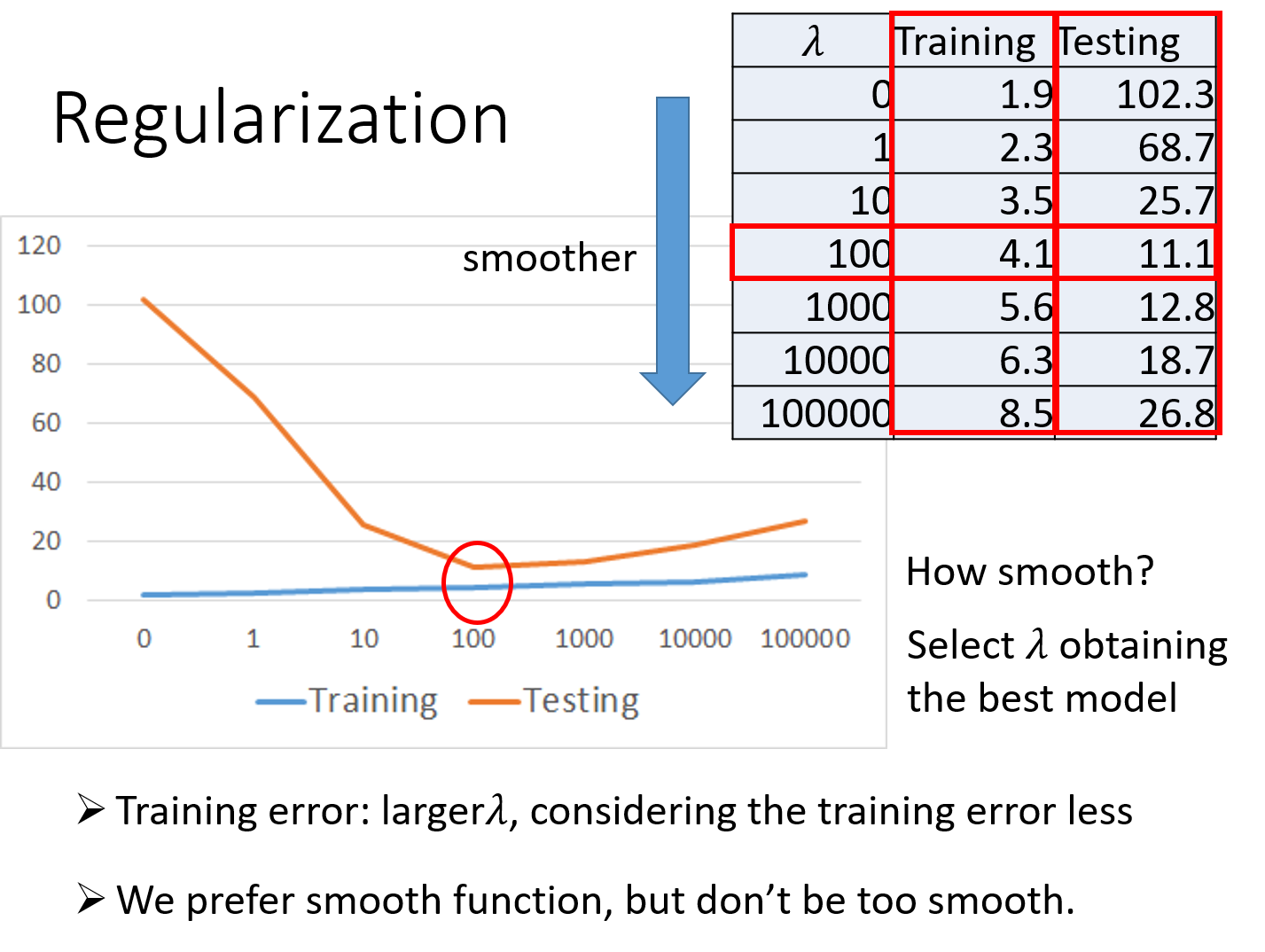
 注:这里的λ需要我们手动去调整以取得最好的值
注:这里的λ需要我们手动去调整以取得最好的值
λ值越大代表考虑smooth的那个regularization那一项的影响力越大,我们找到的function就越平滑
观察下图可知,当我们的λ越大的时候,在training data上得到的error其实是越大的,但是这件事情是非常合理的,因为当λ越大的时候,我们就越倾向于考虑w的值而越少考虑error的大小;但是有趣的是,虽然在training data上得到的error越大,但是在testing data上得到的error可能会是比较小的
下图中,当λ从0到100变大的时候,training error不断变大,testing error反而不断变小;但是当λ太大的时候(>100),在testing data上的error就会越来越大
==我们喜欢比较平滑的function,因为它对noise不那么sensitive;但是我们又不喜欢太平滑的function,因为它就失去了对data拟合的能力;而function的平滑程度,就需要通过调整λ来决定==,就像下图中,当λ=100时,在testing data上的error最小,因此我们选择λ=100
注:这里的error指的是
conclusion总结
关于pokemon的cp值预测的流程总结:
根据已有的data特点(labeled data,包含宝可梦及进化后的cp值),确定使用supervised learning监督学习
根据output的特点(输出的是scalar数值),确定使用regression回归(linear or non-linear)
考虑包括进化前cp值、species、hp等各方面变量属性以及高次项的影响,我们的model可以采用这些input的一次项和二次型之和的形式,如:
而为了保证function的平滑性,loss function应使用regularization,即
,注意bias——参数b对function平滑性无影响,因此不额外再次计入loss function(y的表达式里已包含w、b) 利用gradient descent对regularization版本的loss function进行梯度下降迭代处理,每次迭代都减去L对该参数的微分与learning rate之积,假设所有参数合成一个vector:
,那么每次梯度下降的表达式如下: 当梯度稳定不变时,即
为0时,gradient descent便停止,此时如果采用的model是linear的,那么vector必然落于global minima处(凸函数);如果采用的model是Non-linear的,vector可能会落于local minima处(此时需要采取其他办法获取最佳的function) 假定我们已经通过各种方法到达了global minima的地方,此时的vector:
所确定的那个唯一的function就是在该λ下的最佳 ,即loss最小 这里λ的最佳数值是需要通过我们不断调整来获取的,因此令λ等于0,10,100,1000,...不断使用gradient descent或其他算法得到最佳的parameters:
,并计算出这组参数确定的function—— 对training data和testing data上的error值,直到找到那个使testing data的error最小的λ,(这里一开始λ=0,就是没有使用regularization时的loss function) 注:引入评价
的error机制,令error= ,分别计算该 对training data和testing data(more important)的 大小 先设定λ->确定loss function->找到使loss最小的
->确定function->计算error->重新设定新的λ重复上述步骤->使testing data上的error最小的λ所对应的 所对应的function就是我们能够找到的最佳的function
本章节总结:
Pokémon: Original CP and species almost decide the CP after evolution
There are probably other hidden factors
Gradient descent
- More theory and tips in the following lectures
Overfitting and Regularization
We finally get average error = 11.1 on the testing data
How about new data? Larger error? Lower error?(larger->need validation)
Next lecture: Where does the error come from?
- More theory about overfitting and regularization
- The concept of validation(用来解决new data的error高于11.1的问题)
附:Regularization(L1 L2 正则化解决overfitting)
Regularization -> redefine the loss function
关于overfitting的问题,很大程度上是由于曲线为了更好地拟合training data的数据,而引入了更多的高次项,使得曲线更加“蜿蜒曲折”,反而导致了对testing data的误差更大
回过头来思考,我们之前衡量model中某个function的好坏所使用的loss function,仅引入了真实值和预测值差值的平方和这一个衡量标准;我们想要避免overfitting过拟合的问题,就要使得高次项对曲线形状的影响尽可能小,因此我们要在loss function里引入高次项(非线性部分)的衡量标准,也就是将高次项的系数也加权放进loss function中,这样可以使得训练出来的model既满足预测值和真实值的误差小,又满足高次项的系数尽可能小而使曲线的形状比较稳定集中
以下图为例,如果loss function仅考虑了
或者是说, 蓝色的线最开始时, 和红色线同样也有c、d两个参数, 可是最终学出来时, c 和 d 都学成了0, 虽然蓝色方程的误差要比红色大, 但是概括起数据来还是蓝色好
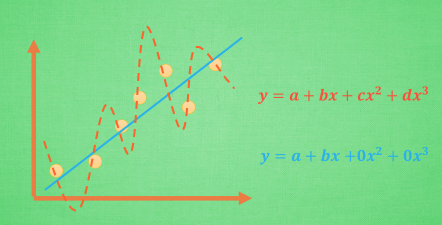 这也是我们通常采用的方法,我们不可能一开始就否定高次项而直接只采用低次线性表达式的model,因为有时候真实数据的确是符合高次项非线性曲线的分布的;而如果一开始直接采用高次非线性表达式的model,就很有可能造成overfitting,在曲线偏折的地方与真实数据的误差非常大。我们的目标应该是这样的:
这也是我们通常采用的方法,我们不可能一开始就否定高次项而直接只采用低次线性表达式的model,因为有时候真实数据的确是符合高次项非线性曲线的分布的;而如果一开始直接采用高次非线性表达式的model,就很有可能造成overfitting,在曲线偏折的地方与真实数据的误差非常大。我们的目标应该是这样的:
==在无法确定真实数据分布的情况下,我们尽可能去改变loss function的评价标准==
- 我们的model的表达式要尽可能的复杂,包含尽可能多的参数和尽可能多的高次非线性项;
- 但是我们的loss function又有能力去控制这条曲线的参数和形状,使之不会出现overfitting过拟合的现象;
- 在真实数据满足高次非线性曲线分布的时候,loss function控制训练出来的高次项的系数比较大,使得到的曲线比较弯折起伏;
- 在真实数据满足低次线性分布的时候,loss function控制训练出来的高次项的系数比较小甚至等于0,使得到的曲线接近linear分布
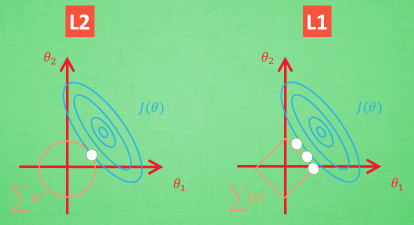
那我们如何保证能学出来这样的参数呢? 这就是 L1 L2 正规化出现的原因.
之前的loss function仅考虑了
L1正规化即加上
这一项,loss function变成 ,即n个training data里的数据的真实值与预测值差值的平方和加上λ权重下的model表达式中所有项系数的绝对值之和 L2正规化即加上
这一项,loss function变成 ,即n个training data里的数据的真实值与预测值差值的平方和加上λ权重下的model表达式中所有项系数的平方和
相对来说,L2要更稳定一些,L1的结果则不那么稳定,如果用p表示正规化程度,上面两式可总结如下: